Квантово-механическая модель атома водорода. Квантовые числа

Вывод о квантовании энергии электрона в атоме водорода по­лучается в

квантовой механике без привлечения постулатов Бора как решение

уравнения Шредингера.

Рассмотрим движение электрона в кулоновском поле ядра, за­ряд которого .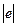

При этом электрон обладает потенциальной энергией где r₁- первый боровский радиус. Состояние электрона описы­вается некоторой волновой функцией, удовлетворяющей урав­нению Шредингера:

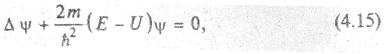
где Е - полная энергия электрона в атоме.

Учитывая, что кулоновское поле ядра, определяющее энергию электрона, центрально-симметрично, целесообразно решать урав­нение Шредингера в сферических координатах r, θ, φ.

При этом функция ψ(х, у, z) переходит в функцию ψ(r, θ, φ), а последняя распадается на три функции R(r), θ(0), Ф(φ).

На искомую волновую функцию наложены естественные усло­вия:

- в каждой точке пространства волновая функция характери­зуется единственным значением;

- значение ψ - функции нигде не обращается в бесконечность;

- ψ - функция есть непрерывная функция координат.

Казалось, что при этих условиях решение уравнения Шре­дингера возможно лишь при целых значениях некоторых пара­метров, от которых зависят функции R, θ, Ф. Опуская математи­ческие выкладки, рассмотрим результаты решения уравнения (4.15) и их физический смысл.

Решение относительно полной энергии электрона Е, связанно­го в атоме, дает дискретный набор значений

где n = 1,2, 3, … .

Таким образом, так же, как и в случае частицы в потенциаль­ной ямс, электрон в атоме находится в дискретных энергетичес­ких состояниях (рис. 4.11). Уровень Е₁ является основным, ос­тальные - возбужденными. При Е < 0 электрон связан в атом при Е > 0 - свободен; в этой области значения энергии изменяются непрерывно. Для отрыва электрона (ионизация атома) надо сообщить электрону извне энергию Е₁..

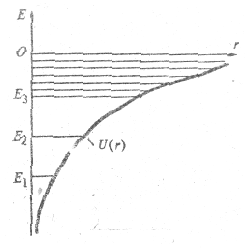Рис. 4.11.

Число n называется главным квантовым числом.

Из решения уравнения (4.15) следует, что момент импульса электрона в атоме также квантуется по формуле

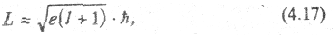
где число l =0, 1, 2, …, n - 1 - называется орбитальным кванто­вым числом.

Проекция момента импульса электрона на некоторое направ­ление z также квантуется:

где число m = -l, -l +1, l -1, l называется магнитным квантовым числом.

Определение расстояния r_i электрона от ядра, соответству­ющего основному состоянию (n = 1), дает значение

совпадающее с первым боровским радиусом.

Было установлено также, что микрообъект (в том числе эле­ктрон) обладает специфической характеристикой, называемой спином. Спин можно интерпретировать как своеобразный мо­мент импульса микрообъекта, не связанный с его движением, не зависящий от внешних условий, неуничтожимый. Квадрат этого момента импульса (не путать с L) равен 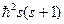, где число s и называется спином. Спин может принимать только целые и полуцелые значения (для электронов, например, s=±1/2). Проекция спинового момента на некоторое направление z принимает зна­чение nσ, где σ=-s, -+1, ..., s-1, s — спиновое квантовое число.

Таким образом, набор квантовых чисел n, l, m, σ , где l, m, σ зависят от значения п, определяется состояние атома. Общее число возможных стационарных состояний N = 2n².