Некоторые случаи решения уравнения Шредингера для движения микрочастиц

Свободное движение частицы (вдоль оси X). В этом случае потенциальная энергия U(x) = 0, и

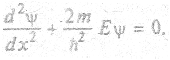
Прямой подстановкой можно убедиться, что частным решени­ем этого уравнения является функция ψ(х) = Ае^ikx, где A = const, k = const.

Значение к определяется из собственного значения энергии

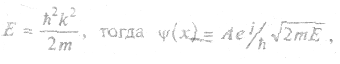что соответствует уравнению плоской монохроматической волны де Бройля, где k имеет смысл волнового числа. Так как k может принять любые значения, энергия свободно движущейся частицы также может быть любой, т. е. изменяться непрерывно. Учтя, что 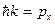, получим зависимость энергии от импульса 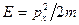, обычную для нерелятивистских частиц. Нахождение частицы в любой точке пространства равновероятно. Вероятность равна |ψ|² = А².

Пространственно-ограниченное движение микрочастицы. Простейший случай такого движения - одномерное движение в так называемой «потенциальной яме» с вертикальными стенками. В этом силовом, поле трафик потен­циальной энергии частицы U(x) имеет следующий виц (рис. 4.6).

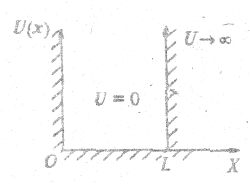
Рис. 4.6.

Частица движется свободно на участке 0 < х < L, где U = 0, а на концах участка сталкивается со стенками, непроницаемость которых выражается в неограниченном возрастании U в точках х = 0, х = L. Понятно, что вероятность обнаружения частицы (а следовательно, и волновая функция) за. пределами «ямы» равна нулю:

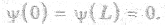
Эти условия называются граничными. Уравнение Шредингера в пределах «ямы» (0 ≤ х ≤ L), где U(x) = 0

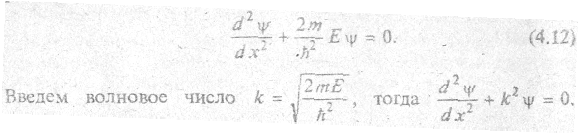
Общее решение такого дифференциального уравнения имеет вид

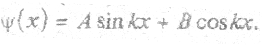
Значения А и В находятся из граничных условий. Так как ψ = 0, то В = 0, и

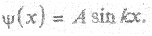
Условие ψ(L) = AsinkL выполняется только при kL = nπ, где n -целые числа, т.е. когда k = nπ,/L. Из равенства

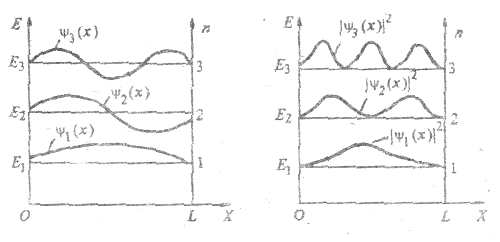
Рис. 4.7.

Таким образом, собственные значения энергии Е_n частицы в данном случае квантованы. Значения Е_n называются энергети­ческими уровнями. На рис. 4.7 представлены графики ψ-функции к плотности вероятности 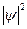для n = 1, 2, 3 (уровней с энергией Е₁, E₂, Е₃). Из графиков, например, следует, что наиболее вероят­ное местонахождение частицы с энергией Е₁ - центр «ямы», а частица с энергией E₂ в середине «ямы», наоборот, находиться не может, а с одинаковой вероятностью находится в ее левой и правой частях.

Важный вывод состоит в том, что пространственное ограниче­ние движения частицы неразрывно связано с количеством ее энергии, и чем меньше объем, в котором частица «заперта», тем заметнее проявляется этот сугубо квантовый эффект. При этом микрочастица не может иметь энергию, меньшую чем Е_min = Е₁. Последнее условие означает невозможность остановки частицы, так как кинетическая энергия ее всегда отлична от нуля. Это положение вытекает и из соотношения неопределенностей. Действительно, с учетом того, что импульс 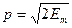, неопреде­ленность Δр импульса не может быть меньше величины 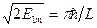. Но ширину «ямы» L можно трактовать как неопределенность координаты: Δх ≈ L. Тогда .

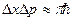С ростом значения п энергетические уровни сближаются и дискретность их сглаживается.

Квантовый осциллятор. Линейным гармоническим осциллято­ром называется частица, массой m, движущаяся вдоль оси X под действием силы F = kх, пропорциональной (k = const) отклоне­нию частицы от положения равновесия (например, пружинный маятник). Потенциальная энергия гармонического осциллятора

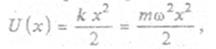
где ω – частота колебаний (рис. 4.8.).

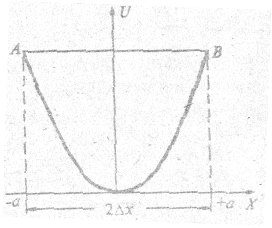
Рис. 4.8.

Амплитуда колебаний осциллятора с классической точки зре­ния определяется запасом его полной энергии Е. В точках А и В потенциальная энергия максимальна (кинетическая равна нулю), в точке 0 - наоборот. Амплитуда ± а ограничивает область нахож­дения осциллирующей частицы.

В квантовой механике учитываются волновые свойства осцил­лирующей частицы, находящейся в потенциальной яме, имеющей вид параболы (рис. 4.9).

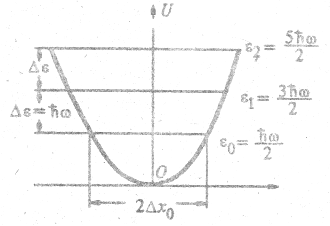
Рис. 4.9.

Решение уравнения Шредингера для этого случая дает следую­щие результаты:

а) энергия осциллятора квантуется:

где n = 0, 1, 2, 3, ...;

б) энергия осциллятора и его амплитуда не может быть равна нулю; минимальная энергия 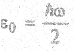(см. рис. 4.9);

с) расстояния между соседними уровнями одинаковы 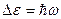, что объясняет существование квантов энергии.

Остановить квантовый осциллятор даже при Т = 0 нельзя. Состояние осциллятора с со называется основным, все другие — возбужденными. Для перевода осциллятора в возбужденные сос­тояния необходимо сообщить ему энергию извне.

Туннельный эффект. Интересной особенностью квантовых час­тил является возможность их прохождения сквозь так называ­емый потенциальный барьер.

Пусть частица обладает энергией Е, меньшей чем потенциаль­ная энергия. U₀ некоторой области («высота» барьера) (рис. 4.10).

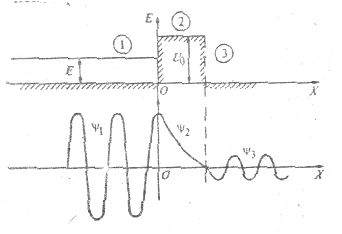
Рис. 4.10.

Классическая частица при таких условиях отразится от барьера и будет двигаться в обратную сторону. Иное дело - квантовая частица. Решение уравнения Шредингера для областей 1, 2, 3 показывает, что волновая функция и внутри барьера (область 2) и за ним (область 3) не равна нулю (рис. 4.9). Это означает, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины. Такой эффект называ­ется туннельным. Возможность этого эффекта также вытекает от соотношения неопределенностей. Если прохождение частицы че­рез барьер происходит в течение времени Δt, то энергия ее харак­теризуется неопределенностью ΔЕ ≥ h/Δt. В случае, если ΔЕ пре­высит высоту" барьера U₀, то частица может через барьер пройти. Туннельный эффект является сугубо квантовым эффектом.