Наибольшее и наименьшее значения функции в замкнутой ограниченной области (глобальный экстремум)
Пусть в замкнутой ограниченной области G определена непрерывная функция и = f(Р). Тогда, как отмечалось в лекции 7, функция и = f(Р) в области G имеет наибольшее и наименьшее значения, т.е. $ точки Р1, Р2 Î G такие, что " РÎG выполняется условие f(Р1) < f(Р) < f(Р2), где f(Р1) = 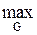 f(Р) и
f(Р) и
f(Р2) = 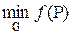 .
.
Очевидно, точки Р1 и Р2 могут лежать как внутри области G, так и на ее границе Г. Если Рi – внутренняя точка, то f(Р) имеет в ней локальный экстремум. Если Рi Î Г, то это точка условного экстремума, где в роли уравнений связи выступают уравнения границы Г. Следовательно, точки глобального экстремума следует искать среди критических точек функции, лежащих внутри области и на ее границе.
Для функции z = f(x, y) двух переменных отыскание наибольшего и наименьшего значений в замкнутой ограниченной области G можно проводить по следующему алгоритму.
1) Найти область определения D(f) функции и проверить, лежит ли область G в D(f).
2) Найти критические точки функции и отобрать из них принадлежащие области G (внутренние критические точки).
На каждом из участков границы Г, используя его уравнение, найти критические точки, записав функцию z = f(x, y) как функцию одной переменной, исключив вторую переменную с помощью уравнением рассматриваемого участка границы. При этом нужно отобрать только те точки, которые принадлежат Г (граничные критические точки).
3) Найти «угловые» точки, т.е. точки соединения отдельных участков границы Г. Вычислить значения функции z = f(x, y) во всех полученных точках и выбрать из них наибольшее и наименьшее.
Замечание. Если область ограничена одной замкнутой линией, то, в случае действий по указанному алгоритму, к угловым точкам следует отнести точки, соответствующие концам отрезка изменения переменной, относительно которой на данной кривой записана заданная функция. Например, для функции 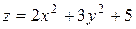 на границе круга
на границе круга 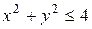 имеет место представление функции в виде
имеет место представление функции в виде 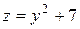 , критическая точка у=0, а граничными точками являются точки (0, 2) и (0, –2), т.к.
, критическая точка у=0, а граничными точками являются точки (0, 2) и (0, –2), т.к. 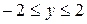 .
.
Пример 4.
Найти наибольшее и наименьшее значения функции z = x2 + y2 в области G, ограниченной линиями у = х2 – 1, у = 3.
Решение. D(z) = R2. Построим область G (рис.7).
Найдем внутренние критические точки:
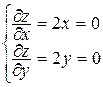 , отсюда Р0(0,0) –критическая точка, причем Р0ÎG.
, отсюда Р0(0,0) –критическая точка, причем Р0ÎG.
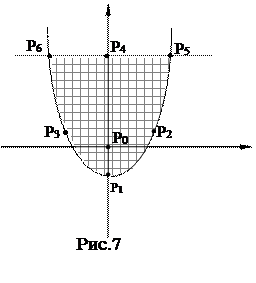 Найдем граничные критические точки. Рассмотрим участок границы, определяемый равенством у = х2 – 1. На этой линии функция z = x2 + y2 может быть записана в виде
Найдем граничные критические точки. Рассмотрим участок границы, определяемый равенством у = х2 – 1. На этой линии функция z = x2 + y2 может быть записана в виде
z1 = x2 + (х2 – 1)2 = х4 – х2 + 1,
тогда z1¢= 4х3 – 2х =2х(2х2 – 1) = 0 , откуда
х = 0, или х = 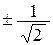 .
.
При х = 0 имеем у = –1 (из равенства у = х2 – 1);
при х = 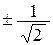 получим у = –
получим у = – 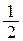 . Получили точки Р1(0, -1), Р2
. Получили точки Р1(0, -1), Р2 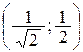 и Р3
и Р3 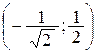 , принадлежащие границе области G (рис.7).
, принадлежащие границе области G (рис.7).
На участке границы, заданном уравнением у = 3, функция z = x2 + y2 может быть записана в виде z2 = x2 + 9, тогда z2¢= 2х = 0, откуда х = 0. Тогда получаем точку Р4(0,3), которая также принадлежит границе области G.
Найдем «угловые» точки, для этого определим точки пересечения участков границы
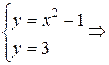 Р5(2, 3) и Р6(–2, 3)
Р5(2, 3) и Р6(–2, 3)
Вычислим значения функции во всех найденных точках.
z(P0) = z(0,0) = 0, z(P1) = z(0,–1) = 1,
z(P2) = z 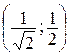 =
= 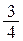 , z(P3) = z
, z(P3) = z 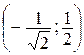 =
= 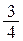
z(P4) = z(0,3) = 9 , z(P5) = z(2,3)= 13, z(P6) = z(–2,3) = 13.
Значит 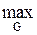 z = z(±2,3)= 13 и
z = z(±2,3)= 13 и 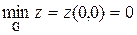 .
.
Мы рассмотрели аналитический метод отыскания глобольного экстремума. Для функции двух переменных может быть также использован графический метод. Суть его в следующем.
Для функции z = f(x, y) строится серия линий уровня f(x, y) = С для значений C0<C1<C2<...<Cn так, чтобы они проходили через заданную область G. Точка Р1ÎG, через которую проходит линия уровня с наименьшим Ск, есть точка наименьшего значения функции в этой области, а наименьшее значение функции равно числу Ск. Точка Р2ÎG, через которую проходит линия уровня с наибольшим Ст, есть точка наибольшего значения функции в области G, а наибольшее значение функции равно Ст.
Пример.5
Найти графически наибольшее и наименьшее значения функции
z = x2 + y – 1 в области G = {y = 0 , x = 1, y = x + 1}.
Решение. Построим область G, это треугольник АВМ.
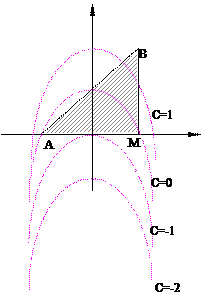 Линии уровня заданной функции имеют уравнения x2 + y – 1 = С. Это есть параболы y = (1 +С) – x2 . Построим серию этих парабол. Имеем
Линии уровня заданной функции имеют уравнения x2 + y – 1 = С. Это есть параболы y = (1 +С) – x2 . Построим серию этих парабол. Имеем
С1 = –2, у = –1– x2 ,
С2 = –1, у = – x2 ,
С3 = 0, у = 1– x2 ,
С4 = 1, у = 2 – x2 , и т.д.
Очевидно, первая точка, через которую линии уровня с возрастанием С «входят» в область, это точка (0,0). Значит, это и есть точка наименьшего значения функции, а так как на линии уровня, проходящей через эту точку, С = –1, то
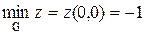 .
.
Последняя точка области G, через которую пройдут линии уровня при возрастании С, будет вершина В треугольника АВМ, ее координаты (1,2), значит, 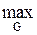 z = z(1, 2) = 2.
z = z(1, 2) = 2.
Замечание.
Если z = f(x, y) – линейная функция, то достаточно построить одну линию уровня, а затем передвигать ее параллельно себе в направлении градиента функции. Точка входа в область (или точка выхода при движении в направлении, противоположном направлению градиента) будет точкой наименьшего значения, а точка выхода – точкой наибольшего значения функции в заданной области.
Пример 6.
Найти наибольшее и наименьшее значения функции z = x + y в области G, ограниченной линиями у = х, у = (х – 2)2.
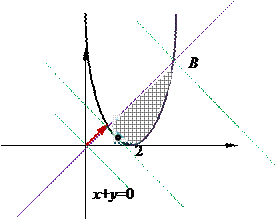 Решение. Построим область G. Функция z = x + y – линейная, значит, ее градиент в любой точке области определения сохраняет направление и равен grad z =
Решение. Построим область G. Функция z = x + y – линейная, значит, ее градиент в любой точке области определения сохраняет направление и равен grad z = 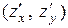 = (1, 1) .
= (1, 1) .
Рассмотрим одну из линий уровня заданной функции
х + у = С,
|
Заметим, что grad z перпендикулярен линии уровня х+у=0. Двигая линию уровня в направлении градиента, найдем точку А входа линий уровня в область G и точку В выхода линий из области. Точка В есть точка пересечения линий, образующих границу области:
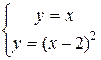 Þ В(4,4).
Þ В(4,4).
Точка А – это точка кривой у = (х– 2)2, в которой касательная параллельна прямой х+ у =0, т.е. прямой у = –х. Тогда угловые коэффициенты этой прямой и касательной совпадают Угловой коэффициент прямой у = –х равен k = –1, а для касательной k = 2(x– 2).
Из равенства 2(x– 2) = –1 находим х = 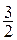 , тогда у =
, тогда у = 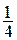 , таким образом,
, таким образом, 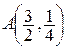 . Тогда
. Тогда 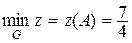 , а
, а 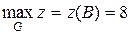 .
.
Дата добавления: 2017-11-21; просмотров: 2597;











