Условный экстремум.
Экстремумы функции нескольких переменных
Содержание лекций: Локальный экстремум. Необходимое и достаточное условия экстремума. Условный экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой ограниченной области.
Метод наименьших квадратов.
Локальный экстремум ФНП
Пусть дана функция и = f(Р), РÎDÌRn и пусть точка Р0(а1, а2, ..., ап) –внутренняя точка множества D.
Определение 9.4.
1) Точка Р0 называется точкой максимума функции и = f(Р), если существует окрестность этой точки U(P0) Ì D такая, что для любой точки Р(х1, х2, ..., хп)Î U(P0) , Р¹Р0, выполняется условие f(P) £ f(P0) . Значение f(P0) функции в точке максимума называется максимумом функции и обозначается f(P0) = max f(P) .
2) Точка Р0 называется точкой минимума функции и = f(Р), если существует окрестность этой точки U(P0)Ì D такая, что для любой точки Р(х1, х2, ..., хп)ÎU(P0), Р¹Р0, выполняется условие f(P) ³ f(P0) . Значение f(P0) функции в точке минимума называется минимумом функции и обозначается f(P0) = min f(P).
Точки минимума и максимума функции называются точками экстремумов, значения функции в точках экстремумов называются экстремумами функции.
Как следует из определения, неравенства f(P) £ f(P0) , f(P) ³ f(P0) должны выполняться только в некоторой окрестности точки Р0 , а не во всей области определения функции, значит, функция может иметь несколько однотипных экстремумов (несколько минимумов, несколько максимумов). Поэтому определенные выше экстремумы называют локальными (местными) экстремумами.
Теорема 9.1.(необходимое условие экстремума ФНП)
Если функция и = f(х1, х2, ..., хп) имеет экстремум в точке Р0, то ее частные производные первого порядка в этой точке либо равны нулю, либо не существуют.
Доказательство. Пусть в точке Р0(а1, а2, ..., ап) функция и = f(P) имеет экстремум, например, максимум. Зафиксируем аргументы х2, ..., хп , положив х2=а2,..., хп = ап. Тогда и = f(P) = f1((х1, а2, ..., ап) есть функция одной переменной х1. Так как эта функция имеет при х1 = а1 экстремум (максимум), то f1¢=0или не существует при х1=а1 (необходимое условие существования экстремума функции одной переменной). Но 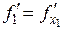 , значит
, значит 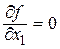 или не существует в точке Р0 – точке экстремума. Аналогично можно рассмотреть частные производные по остальным переменным. ЧТД.
или не существует в точке Р0 – точке экстремума. Аналогично можно рассмотреть частные производные по остальным переменным. ЧТД.
Точки области определения функции, в которых частные производные первого порядка равны нулю или не существуют, называются критическими точками этой функции.
Как следует из теоремы 9.1, точки экстремума ФНП следует искать среди критических точек функции. Но, как и для функции одной переменной, не всякая критическая точка является точкой экстремума.
Теорема 9.2.(достаточное условие экстремума ФНП)
Пусть Р0 – критическая точка функции и = f(P) и 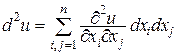 – дифференциал второго порядка этой функции. Тогда
– дифференциал второго порядка этой функции. Тогда
а) если d2u(P0) > 0 при 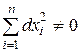 , то Р0 – точка минимума функции и = f(P);
, то Р0 – точка минимума функции и = f(P);
б) если d2u(P0) < 0 при 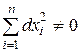 , то Р0 – точка максимума функции и = f(P);
, то Р0 – точка максимума функции и = f(P);
в) если d2u(P0) не определен по знаку, то Р0 не является точкой экстремума;
Эту теорему рассмотрим без доказательства.
Заметим, что в теореме не рассмотрен случай, когда d2u(P0) = 0 или не существует. Это означает, что вопрос о наличие экстремума в точке Р0 при таких условиях остается открытым – нужны дополнительные исследования, например, исследование приращения функции в этой точке.
В более подробных курсах математики доказывается, что в частности для функции z = f(x, y) двух переменных, дифференциал второго порядка которой есть сумма вида
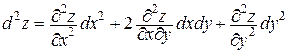
исследование наличия экстремума в критической точке Р0 можно упростить.
Обозначим 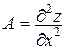 ,
, 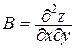 ,
, 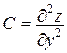 . Составим определитель
. Составим определитель
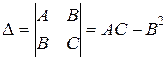 .
.
Оказывается:
d2z > 0 в точке Р0, т.е. Р0 – точка минимума, если A(P0) > 0 и D(Р0) > 0;
d2z < 0 в точке Р0, т.е. Р0 – точка максимума, если A(P0) < 0 , а D(Р0) > 0;
если D(Р0) < 0, то d2z в окрестности точки Р0 меняет знак и экстремума в точке Р0 нет;
если же D(Р0) = 0, то также требуются дополнительные исследования функции в окрестности критической точки Р0.
Таким образом, для функции z = f(x, y) двух переменных имеем следующий алгоритм (назовем его «алгоритмом D») отыскания экстремума:
1) Найти область определения D(f) функции.
2) Найти критические точки, т.е. точки из D(f), для которых 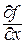 и
и 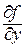 равны нулю или не существуют.
равны нулю или не существуют.
3) В каждой критической точке Р0 проверить достаточные условия экстремума. Для этого найти 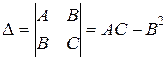 , где
, где 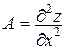 ,
, 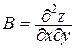 ,
, 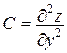 и вычислить D(Р0) и А(Р0).Тогда:
и вычислить D(Р0) и А(Р0).Тогда:
если D(Р0) >0 , то в точке Р0 есть экстремум, причем, если А(Р0) > 0 – то это минимум, а если А(Р0) < 0 – максимум;
если D(Р0) < 0, то в точке Р0 нет экстремума;
Если D(Р0) = 0, то нужны дополнительные исследования.
4) В найденных точках экстремума вычислить значение функции.
Пример1.
Найти экстремум функции z = x3 + 8y3 – 3xy .
Решение. Область определения этой функции – вся координатная плоскость. Найдем критические точки.
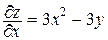 ,
, 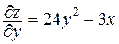 ,
, 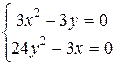 Þ Р0(0,0) ,
Þ Р0(0,0) , 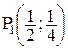 .
.
Проверим выполнение достаточных условий экстремума. Найдем
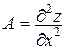 = 6х,
= 6х, 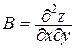 = -3,
= -3, 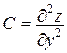 = 48у и
= 48у и 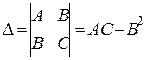 = 288ху – 9.
= 288ху – 9.
Тогда D(Р0) = 288×0×0 – 9 = -9< 0 , значит, в точке Р0 экстремума нет.
D(Р1) = 36-9>0 – в точке Р1 есть экстремум, а так как А(Р1) = 3 >0, то этот экстремум – минимум. Значит, min z= z(P1) = 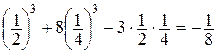 .
.
Пример 2.
Найти экстремум функции 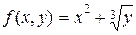 .
.
Решение: D(f) =R2 . Критические точки: 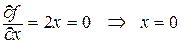 ;
; 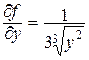 не существует при у = 0, значит Р0(0,0) – критическая точка данной функции.
не существует при у = 0, значит Р0(0,0) – критическая точка данной функции.
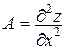 = 2,
= 2, 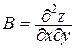 = 0,
= 0, 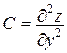 =
= 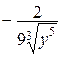 ,
, 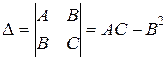 =
= 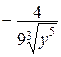 , но D(Р0) не определено, поэтому исследование его знака невозможно.
, но D(Р0) не определено, поэтому исследование его знака невозможно.
По этой же причине невозможно применить теорему 9.2 непосредственно – d2z в этой точке не существует.
Рассмотрим приращение функции f(x, y) в точке Р0. Если Df =f(P) – f(P0)>0 " Р, то Р0 точка минимума, если же Df < 0, то Р0 – точка максимума.
Имеем в нашем случае
Df = f(x, y) – f(0, 0) = f(0+Dx,0+Dy) – f(0, 0) = 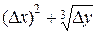 .
.
При Dx = 0,1 и Dy = -0,008 получим Df = 0,01 – 0,2 < 0, а при Dx = 0,1 и Dy = 0,001 Df = 0,01 + 0,1 > 0, т.е. в окрестности точки Р0 не выполняются ни условие Df <0 (т.е. f(x, y) < f(0, 0) и значит, Р0 – не точка максимума), ни условие Df >0 (т.е. f(x, y) > f(0, 0) и тогда Р0 – не точка минимума). Значит, по определению экстремума, данная функция экстремумов не имеет.
Условный экстремум.
Рассмотренный экстремум функции называют безусловным, так как на аргументы функции не налагаются никакие ограничения (условия).
Определение 9.2. Экстремум функции и = f(х1, х2, ... , хп), найденный при условии, что ее аргументы х1, х2, ... , хп удовлетворяют уравнениям j1(х1, х2, ... , хп) = 0, …, jт(х1, х2, ... , хп) = 0, где P (х1, х2, ... , хп) Î D(f), называется условным экстремумом.
Уравнения jk(х1, х2, ... , хп) = 0 , k = 1, 2,..., m, называются уравнениями связи.
Рассмотрим функции z = f(x, y) двух переменных. Если уравнение связи одно, т.е. 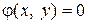 , то отыскание условного экстремума означает, что экстремум ищется не во всей области определения функции, а на некоторой кривой
, то отыскание условного экстремума означает, что экстремум ищется не во всей области определения функции, а на некоторой кривой 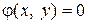 , лежащей в D(f) (т.е. ищутся не самые высокие или самые низкие точки поверхности z = f(x, y), а наиболее высокие или низкие точки среди точек пересечения этой поверхности с цилиндром
, лежащей в D(f) (т.е. ищутся не самые высокие или самые низкие точки поверхности z = f(x, y), а наиболее высокие или низкие точки среди точек пересечения этой поверхности с цилиндром  , рис 5).
, рис 5).
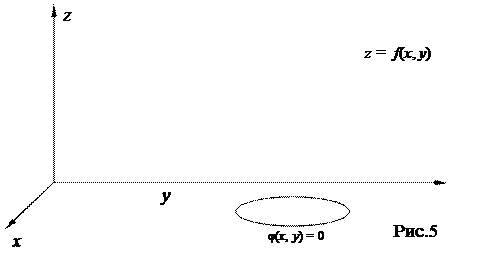
Условный экстремум функции z = f(x, y) двух переменных можно найти следующим способом(метод исключения). Из уравнения 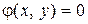 выразить одну из переменных как функцию другой (например, записать
выразить одну из переменных как функцию другой (например, записать 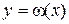 ) и, подставив это значение переменной в функцию
) и, подставив это значение переменной в функцию 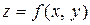 , записать последнюю как функцию одной переменной (в рассмотренном случае
, записать последнюю как функцию одной переменной (в рассмотренном случае 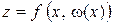 ). Найти экстремум полученной функции одной переменной.
). Найти экстремум полученной функции одной переменной.
Пример 3:
Найти экстремум функции 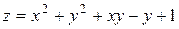 при условии
при условии 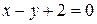 .
.
Решение. Уравнение связи 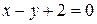 есть линейное уравнение относительно переменных х и у, из которого легко выразить одну переменную через другую, поэтому будем искать условный экстремум данной функции методом исключения.
есть линейное уравнение относительно переменных х и у, из которого легко выразить одну переменную через другую, поэтому будем искать условный экстремум данной функции методом исключения.
Из уравнения 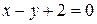 выразим
выразим 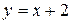 и подставим это выражение в функцию
и подставим это выражение в функцию 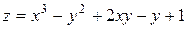 . Получим функцию одной переменной:
. Получим функцию одной переменной:
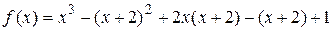 ,
,
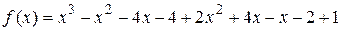 ,
,
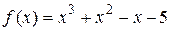 .
.
Найдем экстремумы полученной функции 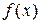 . Область определения этой функции
. Область определения этой функции 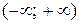 . Находим критические точки:
. Находим критические точки:
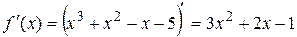 ;
;
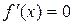 Þ
Þ 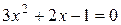 ,
,
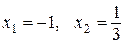 .
.
Проверим наличие экстремума в этих точках (смену знака производной при переходе через эти точки):
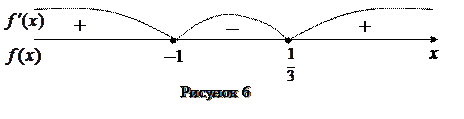 |
Из рисунка 6 видно, что в точке 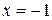 функция
функция 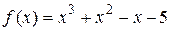 имеет максимум, а в точке
имеет максимум, а в точке 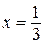 эта функция имеет минимум, причем
эта функция имеет минимум, причем
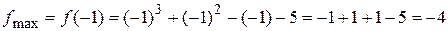 ,
,
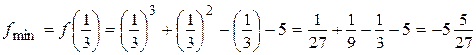 .
.
Но точкам экстремума функции 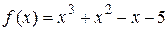 соответствуют точки одноименного условного экстремума исходной функции
соответствуют точки одноименного условного экстремума исходной функции 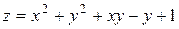 . Найдем координаты этих точек:
. Найдем координаты этих точек:
при 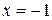 получаем
получаем 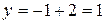 , откуда имеем точку
, откуда имеем точку 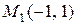 ;
;
при 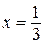 получаем
получаем 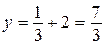 , откуда имеем точку
, откуда имеем точку 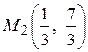 .
.
Таким образом, в точке 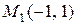 функция
функция 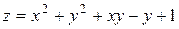 имеет условный максимум
имеет условный максимум
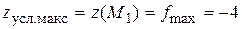 ,
,
а в точке 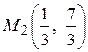 эта функция имеет условный минимум
эта функция имеет условный минимум
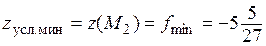 .
.
Дата добавления: 2017-11-21; просмотров: 1843;











