Расчет конических прямозубых передач на контактную прочность

3.77. В основу данного расчета берется формула (3.20) в параметрах эк­вивалентной цилиндрической прямозубой передачи по среднему дополнительно­му конусу

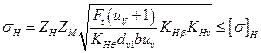
Используем связь тригонометрических функций, формул для определе­ния передаточного числа (см. шаг 3.68) и делительного диаметра эквива­лентного колеса d_vei = d_ei /cosδ₁.

После подстановки в исходную формулу значений d_vl и u_v и несложных преобразований получим формулу проверочного расчета для стальных пря­мозубых конических колес

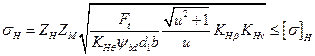(3.30)

или, заменив F_t=2T₂/d₁u; b = Ψ_bdd₁, получим:

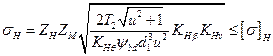
Z = Z_H · Z_M = 462 • 10³ Па^1/2 (для стальных колес), (3.31)

где σ_н — возникающее нормальное контактное напряжение, МПа; d₁ — средний делительный диаметр шестерни, мм; Т₂ — вращающий момент на колесе, Н · мм; Z_H — коэффициент, учитывающий форму сопряжения по­верхности зубьев; Z_M — коэффициент, учитывающий механические свойст­ва материала; Ψ_bd — коэффициент ширины (длины) зуба (см. шаг 3.71); и — передаточное число; К_Hθ = 0,85 — коэффициент, учитывающий снижение контактной прочности конической передачи по сравнению с прямозубой; [σ]_н — допускаемое контактное напряжение (см. шаг 3.45). Из двух значе­ний [σ]_н выбирается меньшее.

Каким образом можно снизить нормальное контактное напряжение в пе­редаче, не изменяя силовых параметров передачи и передаточного числа?

3.78. Проектировочный расчет.

Решая уравнение (3.31) относительно d₁ запишем

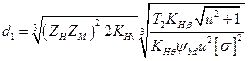
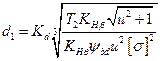(3.32)

где K_d = 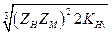— вспомогательный коэффициент (для стальных прямозубых конических колес K_d =78 МПа^1/3); (/„.мм; Т₂, Н • мм; [σ]_н, МПа.

Запишите в конспект формулы для определения[σ]_H.