Цилиндрические прямозубые передачи. Устройство и основные геометрические соотношения
3.29.Зубчатую передачу с параллельными осями, у колес которой поверхности по диаметру выступов цилиндрические, называют цилиндрической.
Цилиндрическая прямозубая зубчатая передача состоит из двух или нескольких пар цилиндрических зубчатых колес с прямыми зубьями (рис. 3.30). Эта передача наиболее проста в изготовлении. Применяется как в открытом, так и в закрытом исполнении.
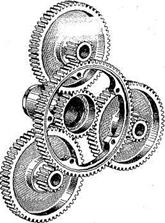
Рис. 3.30. Цилиндрическая прямозубая передача
Передаточное число и ограничивается габаритными размерами передачи. Для одной пары цилиндрических зубчатых колес z2/Z1 = и ≤ 12,5.
Как располагаются оси вращения валов у цилиндрической прямозубой передачи?
3.30.Геометрические соотношения размеров прямозубой цилиндрической передачи с эвольвентным профилем зуба. Определим геометрические параметры прямозубой цилиндрической передачи в зависимости от модуля и числа зубьев (т и z).
Диаметр вершин зубьев da = d + 2ha (рис. 3.31);
диаметр впадин df= d- 2hf.
Из равенства nd = pt z делительный диаметр:
d = (pt/n)z или d= mz 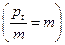 .
.
Согласно стандарту высота головки зуба ha = m; высота ножки зуба hf= 1,25т;
высота зуба h = ha + hf= m +1,25m = 2,25т. Отсюда диаметр вершин зубьев da = mz+ 2m = m(z +2); диаметр впадин df = mz- 2,5m = m(z- 2,5).
Разница в высоте ножки одного колеса и высоте головки другого образует радиальный зазор
с = hf- ha = 1,25m - т = 0,25т
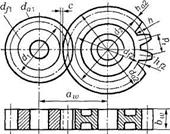
Рис. 3.31.Основные геометрические параметры
передач с эвольвентным профилем зубьев
Межосевое расстояние при а = аω (см. рис. 3.31) аω = {d1 + d2)/2 или аω = (mz16 + mz2)/2.
Приняв суммарное число зубьев z1 + Z2 = z∑ найдем аω = (mz∑)/2.
В прямозубой передаче ширина венца bω равна длине зуба: bω = mΨm, где Ψm— коэффициент длины зуба (ширины венца) по модулю (для цилиндрических прямозубых передач); выбирается по табл. 3.2.
Таблица 3.2. Значение коэффициентаΨm
| Ψm = bω/m, не более | нв | Характеристика конструкции |
| 45-30 30-20 | До 350 Свыше 350 | Высоконагруженные точные передачи. Валы, опоры и корпуса повышенной жесткости |
| 30-25 20-15 15-10 | До 350 Свыше 350 | Обычные передачи редукторного типа в отдельном корпусе с достаточно жесткими валами и опорами. Передачи низкой точности с консольными валами |
Определите модуль т зубчатого колеса с числом зубьев z no известным d1, da, df, aω.
Таблица 3.3. Геометрические параметры прямозубой цилиндрической передачи
| Параметр, обозначение | Расчетные формулы |
| Модуль т | 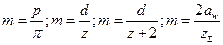
|
| Диаметр вершин зубьев da | da = m(z + 2) |
| Делительный диаметр d | d=mz |
| Диаметр впадин зубьев df | df = m(z- 2,5) |
| Высота зуба h | h = 2,25m |
| Высота головки зуба ha | ha = m |
| Высота ножки зуба hf | hf = 1,25m |
| Окружная толщина зуба s, | 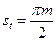
|
| Окружная толщина впадин зубьев е, | 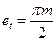
|
| Окончание табл. 3.3 | |
| Параметр, обозначение | Расчетные формулы |
| Радиальный зазор с | с = 0,25т |
| Межосевое расстояние аш | 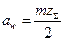
|
| Окружной шаг р, | Pt =πm |
| Длина зуба (ширина венца) Ьш = b | ьω=ь=mΨт |
3.31. Определение числа зубьев шестерни и колеса по суммарному числу зубьев передачи и известному передаточному числу. Если известно и и zz, то число зубьев шестерни и колеса можно определить по формулам:
z1 = z∑/(1 + и); z2 = z∑-z1,
где Z1 — число зубьев шестерни; z2 — число зубьев колеса; z∑ — суммарное число зубьев; и — передаточное число.
Выведите формулы для определения Z1 и Z2 при известных Z∑ и и.
3.32.Ответить на вопросы контрольной карточки 3.5.
Дата добавления: 2017-11-21; просмотров: 8463;











