Движение электронов в периодическом поле кристалла. Уравнение Шредингера для кристалла

В первой главе обсуждалось квантовомеханическое описание свободных микрочастиц или частиц, находящихся во внешнем силовом поле. Однако основные успехи квантовой механики связаны с изучением систем взаимодействующих микрочастиц (электронов, ядер, атомов, молекул), из которых состоит вещество. В этой главе мы применим квантовую механику к описанию поведения электронов в твердых кристаллических телах, рассматривая кристалл как систему микрочастиц.

В общем случае эта задача требует решения уравнения Шредингера для системы частиц (электронов и ядер), образующих кристалл. В этом уравнении необходимо учесть кинетическую энергию всех электронов и ядер, потенциальную энергию взаимодействия электронов между собой, ядер между собой, электронов с ядрами. Понятно, что в общем виде решение такого уравнения не представляется возможным, поскольку оно содержит порядка 10²² переменных. Поэтому задачи, связанные с поведением электронов в кристалле, решаются при некоторых упрощающих допущениях (приближениях), правомерность которых определяется конкретными свойствами кристалла. Рассмотрим основные из этих допущений.

Адиабатическое приближение. В этом приближении предполагается, что электроны движутся в поле неподвижных ядер. Под ядрами здесь подразумевают собственно ядра атомов со всеми электронам, исключая валентные. Правомерность этого допущения определяется тем, что скорости электронов приблизительно на два порядка больше, чем скорости ядер, поэтому для любой, даже неравновесной конфигурации ядер всегда будет успевать устанавливаться соответствующее ей электронное равновесие. В этом представлении исключается обмен энергией между электронной и ядерной системами, поэтому это приближение называется адиабатическим. Естественно, что в адиабатическом приближении нельзя рассматривать такие явления, как диффузия, ионная проводимость и др., связанные с движением атомов или ионов.

Одноэлектронное приближение.В этом приближении вместо взаимодействия данного электрона с остальными электронами и ядрами по отдельности рассматривают его движение в некотором результирующем усредненном поле остальных электронов и ядер. Такое поле называют самосогласованным. В одноэлектронном приближении, таким образом, задача сводится к независимому описанию каждого электрона в среднем внешнем поле с потенциальной энергией U(r). Вид функции U(r) определяется свойствами симметрии кристалла. Основное свойство самосогласованного поля заключается в том, что оно имеет тот же период, что и поле ядер.

Таким образом, адиабатическое и одноэлектронное приближение приводит к задаче движения электрона в некотором периодическом потенциальном поле, имеющем период, равный постоянной решетки кристалла. Уравнение Шредингера в этом случае будет иметь вид

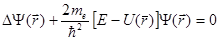. (2.1)

Здесь 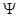(r) - волновая функция электрона, 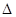- оператор Лапласа, m_e - масса электрона, Е - энергия электрона в кристалле.

Следующие два допущения связаны с невозможностью точно определить вид функции U(r). Поэтому обычно при описании свойств электронов в кристалле рассматривают два предельных случая взаимодействия электронов с решеткой.

Приближение слабой связи. В этом приближении электроны в кристалле рассматривают как почти свободные частицы, на движение которых оказывает слабое возмущение поле кристаллической решетки. Данное допущение применимо, когда потенциальная энергия взаимодействия электрона с решеткой много меньше его кинетической энергии. Такой подход, который иногда называют "приближением почти свободных электронов", позволяет получить решение некоторых задач, связанных с поведением валентных электронов в металлах.

В полупроводниках более приемлемым для анализа их физических свойств является приближение сильной связи. В этом приближении состояние электрона в кристалле мало отличается от его состояния в изолированном атоме. Приближение сильной связи применимо, когда потенциальная энергия электрона значительно больше его кинетической энергии.

Характерным для обоих приближений слабой и сильной связи является то, что оба они приводят к фундаментальному свойству энергетического распределения электронов в кристалле - возникновению разрешенных и запрещенных энергетических зон.