Импульсная характеристика и передаточная функция согласованного фильтра

Существует большой класс задач, в которых требуется обнаружить сигнал, если форма его известна.

Примеры:

1) Прием телеграфных сигналов ( прямоугольной формы).

2) Сигналы ИКМ.

3) Радиолокационные сигналы.

Во всех этих случаях важным параметром, характеризующим качество обнаружения, является отношение 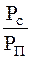. Линейный фильтр, максимизирующий 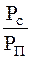называется оптимальным согласованным фильтром.

Идея: на фоне помех сигнал легче обнаружить, если он имеет импульсный характер и по амплитуде превышает помехи. Качество обнаружения будет тем лучше, чем больше .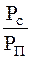

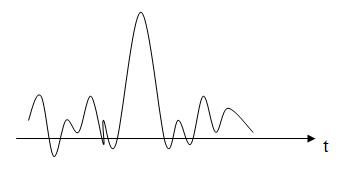
Рис.1. Произвольная форма сигнала

Основная операция, которую выполняет оптимальный когерентный приемник, как было показано в предыдущей лекции - вычисление скалярного произведения между принимаемым случайным процессом 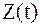и опорным сигналом :

;

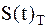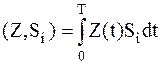(1.1)

Однако выражение (1) можно вычислить не только с помощью коррелятора, но и на основе пассивного линейного фильтра с постоянными параметрами.

Среди таких фильтров представляют интерес фильтры, которые обладают такой передаточной функцией 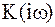, что в момент 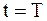, т.е при снятии отсчета .

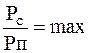1. На выходе СФ действует:

Прием полезный сигнал в данном случае будем рассматривать не как случайный процесс, а как известную функцию с СПМ:

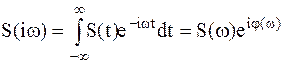;	(1.2)
где		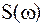и		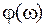–	амплитудный и частотный спектры сигнала

2. Помеху будем считать стационарным СП типа БШ со спектральной плотностью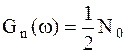

3. Коэффициент передачи линейного фильтра запишем в виде:

;

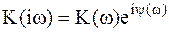(1.3)

Необходимо определить:

а) АЧХ и ФЧХ СФ, при которых 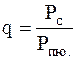на выходе максимальны.

В ТЭС доказано:

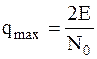;	(1.4)
где		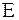–	энергия сигнала
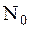
		–	Удельная мощность помехи

б) 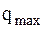достигается только в том случае, если:

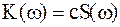;	(1.5)
где		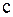–	произвольный коэффициент пропорциональности
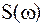
		–	АЧС сигнала

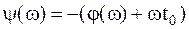;	(1.6)
где		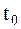–	момент времени, при котором амплитуда сигнала на выходе СФ принимает максимальное значение (задержка в фильтре)

Выводы:

1. АЧХ СФ с точностью до постоянного множителя совпадает с амплитудным спектром сигнала.

2. ФЧХ СФ определяется фазовым спектром сигнала и линейной функцией частоты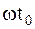

Таким образом, частотная характеристика оптимального фильтра полностью определяется спектром сигнала, т.е. «согласованна» с ним.

Отсюда и название – согласованный фильтр.

Ответим на вопрос: почему СФ дает 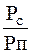мах на выходе.

Как это объяснить физически?

Для ответа на данный вопрос определим фазу сигнала на выходе СФ

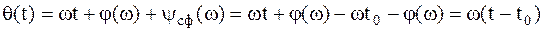
(1.7)

Итак, при 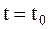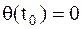т.е. в момент 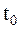все гармонические составляющие сигнала имеют одинаковую фазу и складываются арифметически, образуя в этот момент пик сигнала на выходе. Спектральные составляющие помехи на выходе СФ имеют случайную величину. Именно поэтому СФ максимизирует.