Спектр дискретного сигнала

Структурная схема СПИ с использованием устройств ЦОС

Под цифровой обработкой сигналов (ЦОС) понимают операции над дискретными по времени величинами (отсчетами сигналов).

Сигналы на входе и выходе СПИ с ЦОС дискретны не только во времени, но и по уровню, т.е. являются цифровыми сигналами.

Системы с ЦОС имеют преимущества перед аналоговой обработкой:

- более высокая точность обработки сигналов по сложным алгоритмам;

- возможность гибкой перестройки алгоритмов;

- высокая технологичность изготовления устройств ЦОС;

- автоматизация проектирования ЦОС.

Структурная схема СПИ с ЦОС имеет вид:

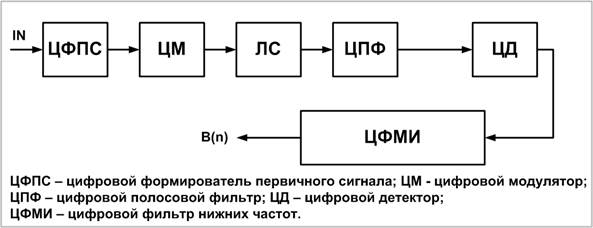
Рисунок 1 – Структурная схема передачи сообщений с использованием ЦОС

Условные обозначения:

1. ЦФПС – цифровой формирователь первичного сигнала;

2. ЦМ - цифровой модулятор;

3. ЦПФ – цифровой полосовой фильтр;

4. ЦД – цифровой детектор;

5. ЦФМИ – цифровой фильтр нижних частот.

  Наибольшее применение нашли линейные системы ЦОС.

Спектр дискретного сигнала

Преобразование Фурье позволяет вычислить спектральную плотность сигнала, представляющего собой функцию (как правило, времени либо пространственных координат).

Дискретный же сигнал является последовательностью чисел, поэтому для анализа его спектра обычными (аналоговыми) средствами необходимо сопоставить этой последовательности некоторую функцию. Традиционным способом такого сопоставления является представление отчетов в виде дельта-функций с соответствующими множителями и задержками.

Для последовательности отчетов 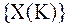получается следующий сигнал:

;

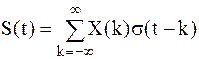(1.1)

Преобразование Фурье линейно, спектр дельта-функции равен единице, а задержка сигнала во времени приводит к умножению спектра на комплексную экспоненту:

;

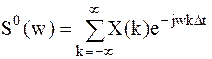(1.2)

Из формулы((1.2)– спектр дискретного сигнала.)) видно главное свойство спектра любого дискретного сигнала: спектр является периодическим, его период в данном случае равен 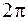(т.е. круговой частоте дискретизации, поскольку, составляя сигнал из дельта-функций, мы выбрали единичный интервал между ними, что даёт ):

;

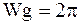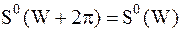(1.3)

Следует также обратить внимание на размерность спектральной функции дискретного сигнала: она совпадает с размерностью отчетов. Это связано с тем, что дельта-функции времени, из которых составлен сигнал, имеет размерность частоты.

Формула (1.2) позволяет вычислить спектральную функцию по известным отсчетам.

Теперь рассмотрим несколько иную задачу. Пусть значения 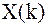являются отсчетами аналогового сигнала 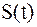, взятыми с периодом .

;

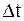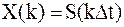(1.4)

Выясним, как в этом случае спектр дискретного сигнала связан со спектром аналогового сигнала.

Итак, мы рассматриваем дискретизированный сигнал в виде последовательностей дельта-функций, «взвешенной» значениями отчетов 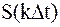аналогового сигнала :

;

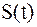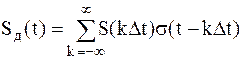(1.5)

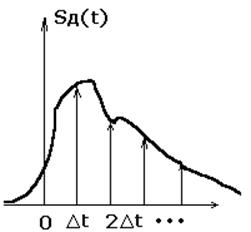
Рис.2. Дискретизированный сигнал в виде последовательностей дельта-функций

Так как функция 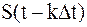равна нулю всюду, кроме момента в выражении (1.5) константа 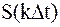на исходный непрерывный сигнал .

;

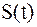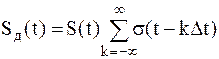(1.6)

Следует отметить, что сумма в (1.6) является периодическим сигналом, а поэтому может быть представлена в виде ряда Фурье.

Коэффициенты этого ряда:

;

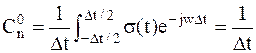(1.7)

В формуле (1.7) было учтено, что в интервал интегрирования 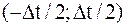попадает только одна дельта-функция, соответствующая .

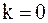Таким образом, периодическая последовательность дельта-функций может быть представлена в виде комплексного ряда Фурье:

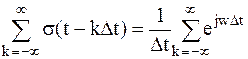;	(1.8)
где		=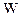

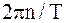
Умножение сигнала на 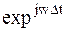соответствует сдвигу спектральной функции на 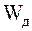, поэтому спектр дискретизированного сигнала можно записать в виде:

;

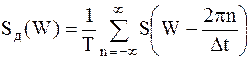(1.9)

Таким образом, спектр дискретизированного сигнала представляет собой бесконечный ряд сдвинутых копий исходного непрерывного сигнала 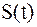. Расстояние по частоте между соседними копиями спектра равно частоте дискретизации.

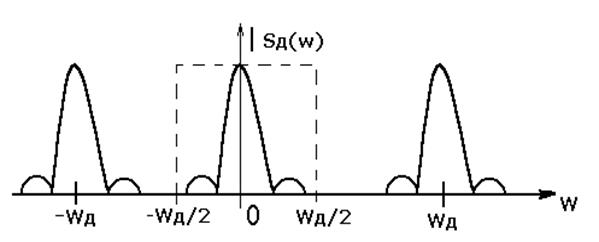
Рис.3 Спектр дискретизированного сигнала

Следует отметить, что из-за наличия в формуле (1.9) множителя 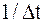спектр дискретизированного сигнала имеет размерность, совпадающую с размерностью сигнала (т.к. 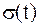имеет размерность частоты).

Характер спектра дискретизированного сигнала ещё раз демонстрирует частотно – временную дуальность преобразования Фурье:

- периодический сигнал – дискретный спектр;

- периодический спектр – дискретный сигнал.

Удобным способом анализа дискретных последовательностей является 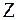– преобразование, ( 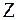– transform).

Смысл его заключается в том, что последовательности чисел 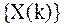ставится в соответствие функции комплексной переменной 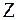, определяемая следующим образом:

;

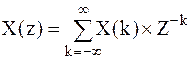(1.10)

Разумеется, функция 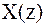определена только для тех значений 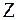, при которых ряд (1.10) сходится, 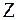– преобразование играет для дискретных сигналов и систем такую же роль, как преобразование Лапласа – для аналоговых.

Определяющим при этом является тот факт, что 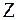– преобразование импульсной характеристики дискретной системы является дробно-рациональной функцией переменной .

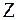Примеры вычисления Z-преобразования:

1) Единичная импульсная функция.

ЕИФ – является дискретным аналогом дельта-функции и представляет собой одиночный отсчёт с единичным значением:

;

;

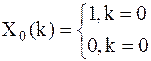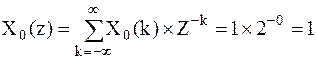Функция 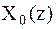сходится на всей комплексной плоскости.

2) Единичный скачок:

;

;

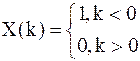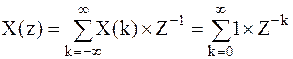Данный ряд является суммой бесконечной геометрической прогрессии с первым членом 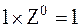и знаменателем .

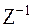Как известно, такой ряд сходится при 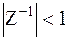, то есть при 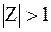, и его сумма равна:

;

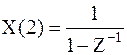3) Алгоритм быстрого преобразования Фурье:

Дискретное преобразование Фурье:

;
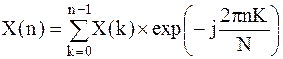где		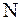–	период

Для вычисления одного коэффициента ДПФ по данной формуле необходимо выполнить N комплексных умножений и сложений.

Таким образом, расчет всего ДПФ, содержащего Nкоэффициентов потребует 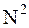пар операций (умножение – сложение). Число операций возрастает пропорционально размерности ДПФ.

Однако, если N не является простым числом и может быть разложено на множители, процесс вычислений можно ускорить, разделив анализируемый набор отсчетов на часы, вычислив их ДПФ и объединив результаты.

Такие способы вычисления ДПФ называют быстрым преобразованием Фурье.

При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге.

(основание БПФ).

Выводы:

1. Устройства ЦОС имеют преимущества перед устройствами обработки сигналов в непрерывном времени.

2. Спектр дискретного сигнала является периодической функцией частоты дискретизации.

3. Существуют методы быстрого преобразования Фурье, позволяющие существенно сократить число операций, выполняемых при расчете ЦФ спектральными методами.