Перспективно-аффинные преобразования

Приведем пример аффинного преобразования, которое не является подобием.

О п р е д е л е н и е. Перспективно-аффинным преобразованием или родством называется нетождественное аффинное преобразование, имеющее по крайней мере две неподвижные точки.

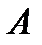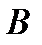Пусть и неподвижные точки родства. Репер 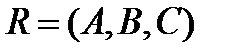при родстве перейдет в репер 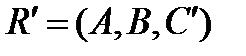., причем 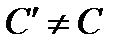(почему?). Пусть 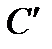имеет в репере 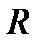координаты 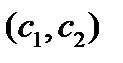. Тогда учитывая, что точка 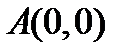переходит в точку 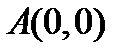, точка 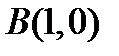переходит в 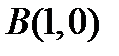, точка 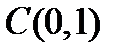переходит в 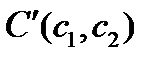, из формул аффинного преобразования получаем:

.

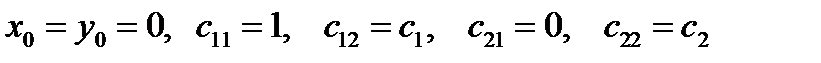Тогда формулы родства принимают вид:

(*)

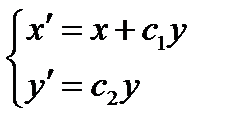Из этих формул получаем свойства родства:

1. Любая точка прямой, проходящей через неподвижные точки родства, является неподвижной точкой. Эта прямая неподвижных точек называется осью родства. Из следствия теоремы о задании аффинного преобразования парой соответствующих аффинных реперов, получаем, что все неподвижные точки родства лежат на его оси.

2. Прямые, соединяющие соответствующие точки родства, не лежащие на его оси, параллельны или совпадают. Действительно, если точка 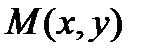перешла в точку 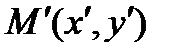, то учитывая формулы (*), получим 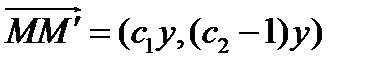. То есть прямая 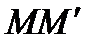, соединяющая соответствующие точки родства, параллельна вектору .

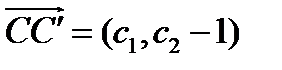Если прямые, соединяющие соответствующие точки родства, не параллельны оси родства, то оно называется косым сжатием плоскости.

Если прямые, соединяющие соответствующие точки родства, параллельны оси родства, то оно называется сдвигом плоскости.

3. Если прямая пересекает ось родства, то её образ проходит через эту точку пересечения; если прямая параллельна оси родства, то её образ тоже параллелен оси родства.

У п р а ж н е н и е. Постройте образ произвольной точки плоскости при родстве, заданном осью и парой соответствующих точек.