Тема 5. Средние величины
1. Понятие и расчет средних величин
2. Свойства средних величин
3. Структурные средние величины
1. Средняя величина - обобщающий показатель, который выражает типичные черты и дает обобщающую количественную характеристику какого-либо уровня какого-либо варьирующего признака по совокупности однородных явлений.
Введем следующие понятия и обозначения:
признак, по которому находится средняя, называется осредняемым признаком и обозначается 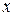 ;
;
величина осредняемого признака у каждой единицы совокупности называется индивидуальным его значением, или вариантами, и обозначается как 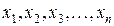 ;
;
частота – это повторяемость индивидуальных значений признака, обозначается буквой f.
В статистике применяют различные виды средних величин:
1) простые (невзвешенные) – когда отдельные значения изучаемой совокупности не повторяются;
2) взвешенные – когда отдельные значения изучаемой совокупности повторяются.
Средняя арифметическая простая – наиболее распространенный вид средней. Она исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.
В зависимости от характера исходных данных средняя арифметическая 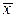 определяется следующим образом.
определяется следующим образом.
Пример 1. Предположим, что требуется вычислить средний стаж десяти работников торгового предприятия 6, 5, 4, 3, 3, 4, 5, 4, 5, 4, т.е. дан ряд одиночных значений признака, тогда х рассчитывается как
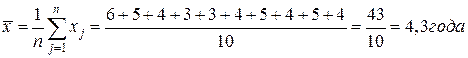 ,
,
т.е. как средняя арифметическая невзвешенная делением количества свободного признака на число показаний:
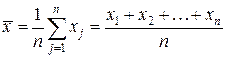 .
.
Часто приходится рассчитывать среднее значение признака по ряду распределения, когда одно и то же значение признака встречается несколько раз. Объединив данные по величине признака (т.е. сгруппировав) и подсчитав число случаев повторения каждого из них, мы получим следующую таблицу.
Продолжительность
стажа работы
(варианты)
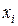
| Число работников торгового предприятия
(частоты)
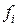
| Отработано человеко-лет
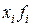
|
| Итого: |
Тогда средняя вычисляется по формуле средней арифметической взвешенной:
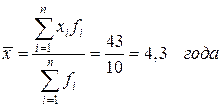 .
.
Часто вычисление средних величин приходится производить и по данным, сгруппированным в виде интервальных рядов распределения, когда варианты признака, из которых исчисляется средняя, представлены в виде интервалов (от – до).
Для вычисления средней величины надо в каждом интервале определить серединное значение 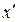 , после чего произвести взвешивание обычным порядком x'f. В закрытом интервале серединное значение определяется как полусумма значений нижней и верхней границ. Иногда задача исчисления средней по величинам интервального ряда осложняется тем, что неизвестны крайние границы начального и конечного интервалов. В этом случае предполагается, что расстояние между границами данного интервала такое же, как и в соседнем интервале.
, после чего произвести взвешивание обычным порядком x'f. В закрытом интервале серединное значение определяется как полусумма значений нижней и верхней границ. Иногда задача исчисления средней по величинам интервального ряда осложняется тем, что неизвестны крайние границы начального и конечного интервалов. В этом случае предполагается, что расстояние между границами данного интервала такое же, как и в соседнем интервале.
Группы предприятий
по объему товарооборота, млн. руб. 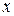
| Число предприятий,
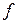
| Середина интервала,
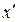
| 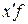
|
| До 400 400-500 500-600 600-700 Свыше 700 | |||
| Итого: |
Пример 2. Объем товарооборота в среднем на одно предприятие составит:
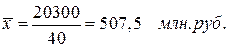
В данном случае для расчета применялась средняя арифметическая взвешенная из интервального ряда.
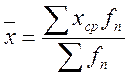 ; где
; где
X ср – серединное значение интервала.
Необходимо отметить, что изложенный прием исчисления средней является вынужденным в том случае, когда нет прямых данных о конкретной величине отдельных вариантов. Этот прием основан на предположении, что отдельные конкретные варианты равномерно распределены внутри интервала. Однако в действительности распределение отдельных вариантов в пределах интервала может оказаться неравномерным, и тогда середина интервала будет в той или иной степени отличаться от принятой средней. Это может повлиять на правильность общей средней, исчисленной по данным интервального ряда.
Необходимо отметить, что, хотя мы и используем для расчета средней из интервального ряда формулу средней арифметической взвешенной, исчисленная средняя не является точной величиной, так как в результате умножения средних значений групп на их численность мы не получим действительного значения. Сходство исчисленной средней со средней взвешенной лишь в методе вычисления. Здесь взяты не индивидуальные значения вариант, а условные средние каждой группы. Их взвешивание имеет чисто формальный характер.
Степень расхождения зависит от ряда причин:
1) число вариант: Чем больше число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Если же на каждую группу приходится малое число единиц, групповые средние могут находиться не только в середине, но и вблизи верхней либо нижней границы интервала. Если же наблюдений много и они более или менее равномерно распределяются в пределах интервала, то средняя величина в группе будет приближаться к середине интервала.
2) величина интервала: Если интервал невелик, то и ошибка будет незначительной, так как фактически групповая средняя будет мало отличаться от середины интервала.
3) характер распределения: Чем симметричнее распределение, тем ошибка меньше.
4) принцип построения интервального ряда: При равных интервалах середина построения его будет ближе примыкать к средней по данной группе. Кроме того, при наличии открытых интервалов к этому добавляются неточности, связанные с условным установлением неизвестных границ.
Средняя гармоническая– это величина, обратная средней арифметической. Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной
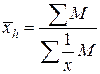 ,
,
где 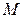 – величина общего объема, т.е.
– величина общего объема, т.е. 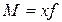 ).
).
Так, например, расчет средней цены выражается отношением: 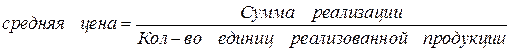 .
.
Пример 4.
| Город | Цена, руб. 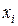
| Сумма реализации, тыс.руб.
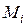
| Частоты
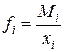
|
| А Б В | |||
| Итого: |
Величина суммы реализации, т. е. показателя, который находится в числителе исходного отношения, известна. Для определения неизвестной величины – количества реализованных единиц – нужно отдельно по каждому виду товара разделить сумму реализации на цену:
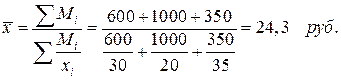
При определении средней цены, используя невзвешенную среднюю арифметическую, получим среднюю, которая не отражает объема реализации,
т.е. нереальна:
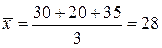 .
.
Как видно, средняя гармоническая является превращенной формой арифметической средней. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака.
В том случае, если объемы явлений, т. е. произведения, по каждому признаку равны, применяется средняя гармоническая (простая).
Пример 5. Две автомашины прошли один и тот же путь: одна со скоростью 60 км/ч, а вторая – 80 км/ч, тогда средняя скорость составит:
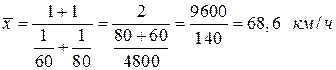 , т.е.
, т.е. 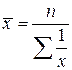 .
.
Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел. Поэтому средняя геометрическая используется в расчетах среднегодовых темпов роста.
Дата добавления: 2021-09-25; просмотров: 457;











