Последовательное соединение восстанавливаемых элементов

Последовательное соединение восстанавливаемых элементов, рассмотрим на примере двух элементов, соединенных последовательно и образующих общую цепь (рис. 1.4).

Пусть p_i – вероятность безотказной работы элемента цепи и является вероятностью того, что в заданный момент времени элемент будет исправлен, то есть он будет в рабочем состоянии, а q_i – вероятность отказа элемента цепи, выражающий среднюю относительную долю года, в течении которого элемент находился в поврежденном состоянии, во время восстановления.

Х2

Х1

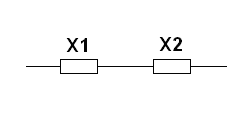
Рис. 1.4. Два последовательно соединенные восстанавливаемые элемента системы электроснабжения

Для двух элементов будут справедливы следующие математические рассуждения:

(р₁+q₁)(p₂+q₂)=1;

p₁p₂+p₁q₂+p₂q₁+q₁q₂=1.

Состояния p₁q₂, p₂q₁ q₁q₂ соответствуют нерабочему состоянию системы, поэтому можно записать:

q=1 – p₁p₂.

Расписывая последнюю формулу, получаем:

q=1-(1-q₁)(1-q₂) = q₁ + q₂ – q₁q₂ .

Произведение q₁q₂ << 1, и им можно пренебречь, тогда Q_ц = q₁ + q₂, где Q_ц - вероятность отказа последовательной цепи элементов

Это будет справедливо и для n соединенных последовательно соединенных элементов

Q_ц = q₁ + q₂ + … + q_n . (1.35)

Для потока отказов цепи ω_ц среднее время между отказами или время наработки на отказ:

Т_ср = 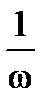или Т_ср = 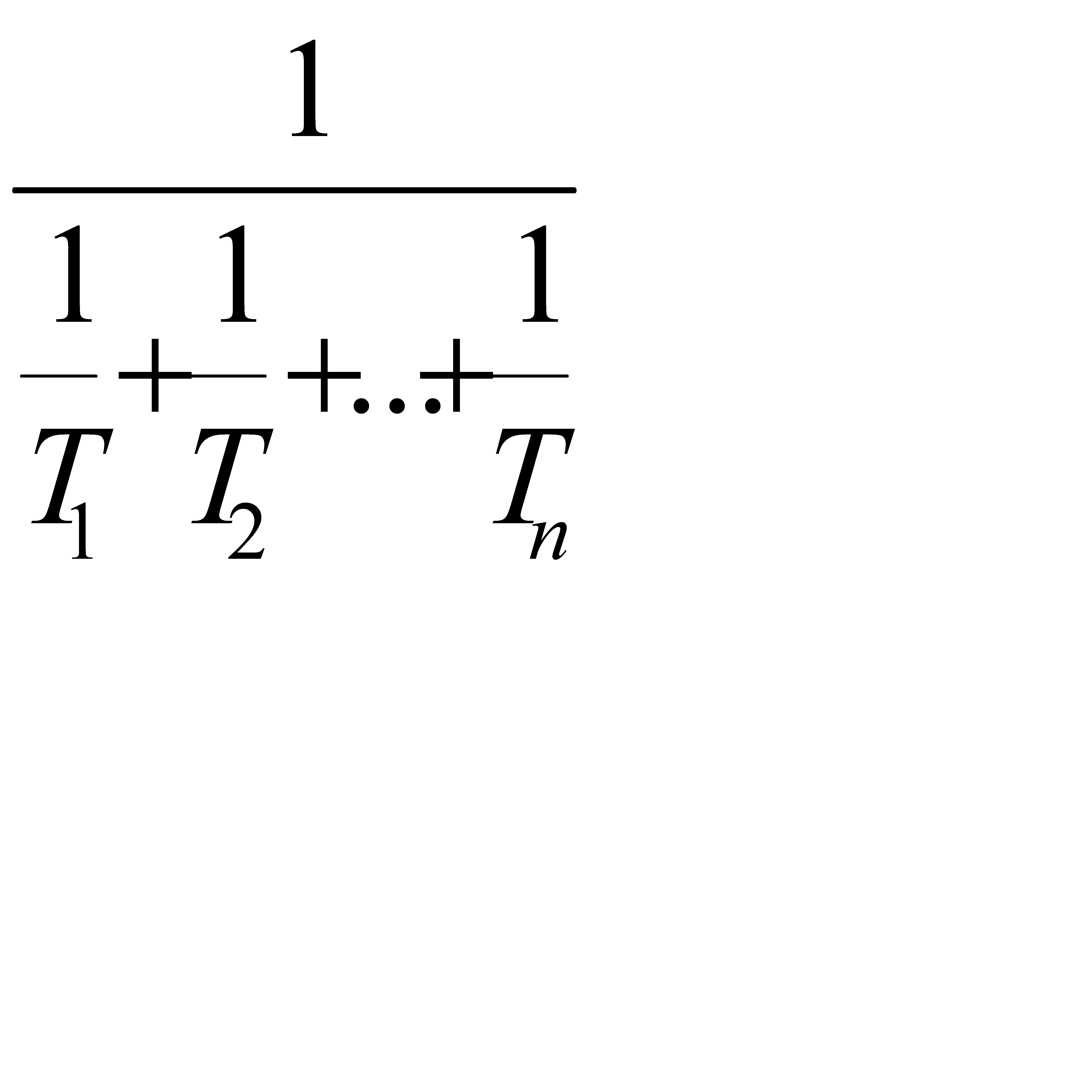(1.36)

Если объекты характеризуются одинаковыми показателями потока отказов, то есть ω₁ = ω₂ = ω, то Т_ср = 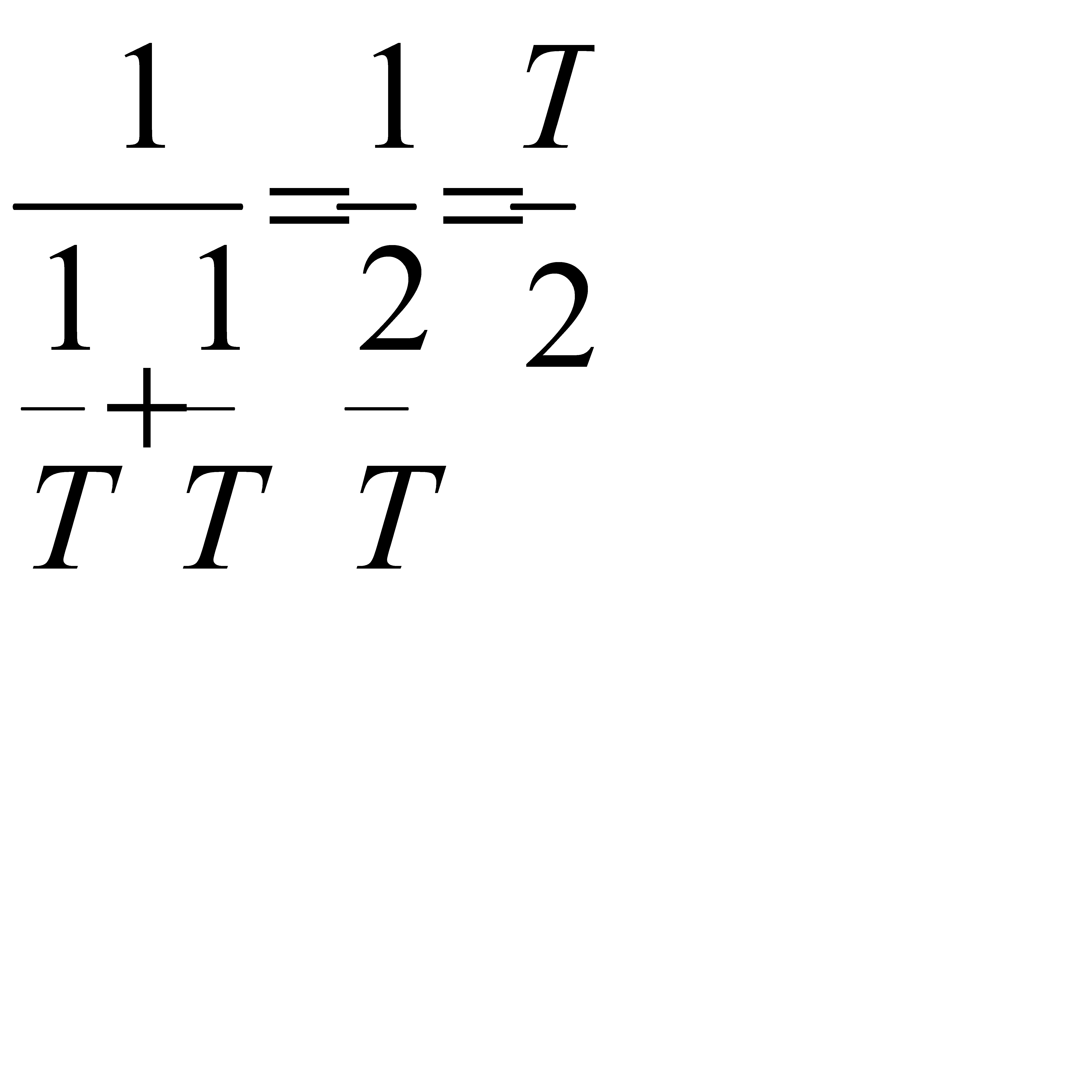- то есть с ростом элементов время рабочего состояния падает.