Последовательное соединение элементов систем электроснабжения

Последовательное соединение элементов является частым соединением элементов в электроснабжении. В понятии отказа заложен физический аналог электрической схемы с последовательным включением элементов (рис.1.3).

Рис. 1.3. Последовательное соединение элементов

Предположим, что система состоит из n последовательно включенных элементов (рис. 1.3). Из теории вероятностей известно, что если определены вероятности появления нескольких независимых случайных событий, то совпадение этих событий определяется как произведение вероятностей их появлений. Система будет находиться в работоспособном состоянии только при условии совпадения работоспособных состояний всех элементов. Таким образом, работоспособность системы оценивается как произведение вероятностей безотказной работы элементов:

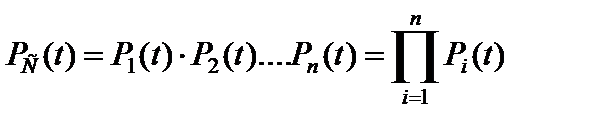, (1.29)

где 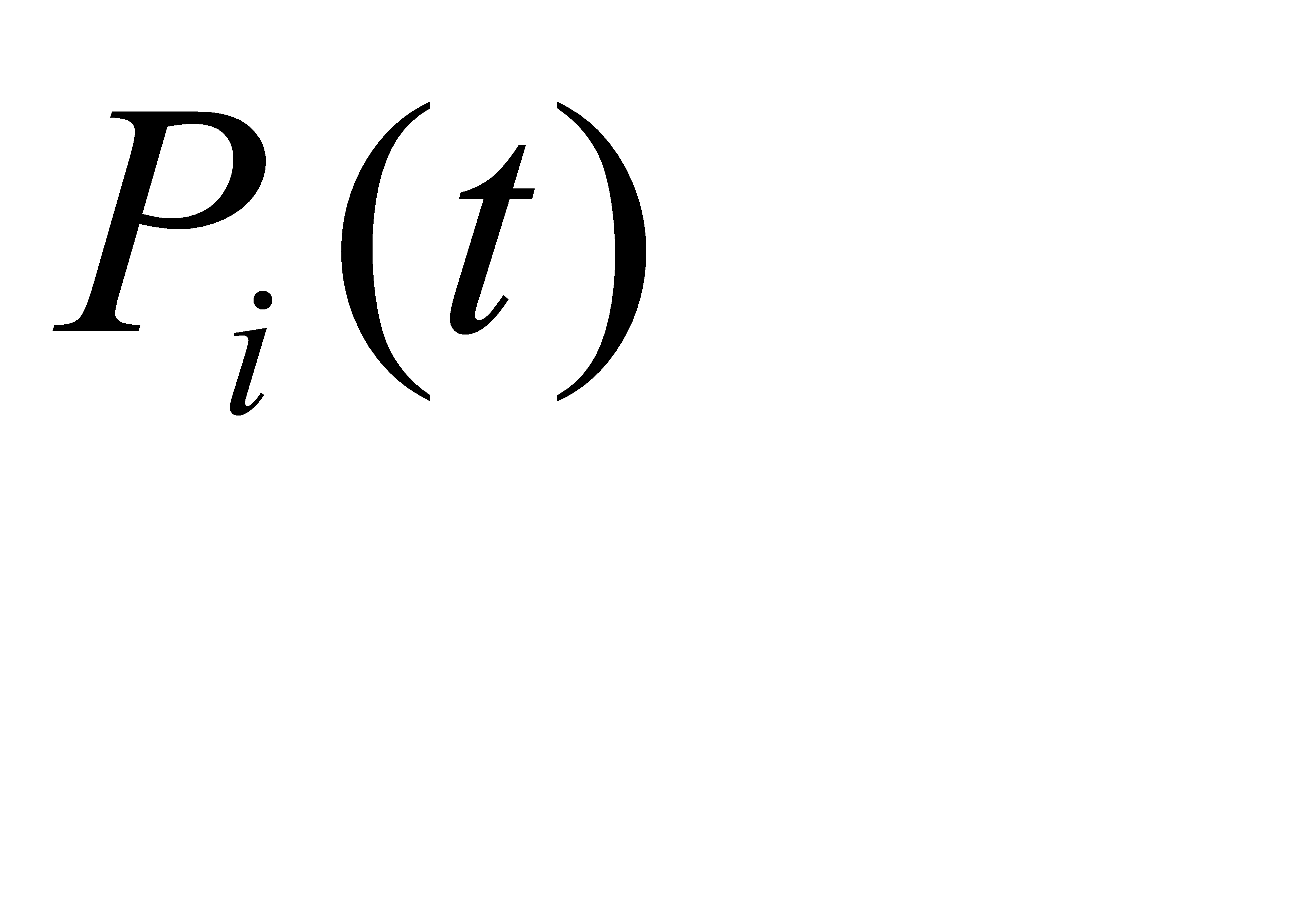- вероятность безотказной работы i-го элемента.

Полагая 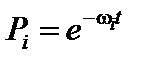, имеем

Р_С= 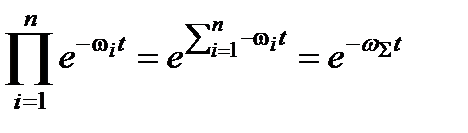, (1.30)

где ω _Σ= ω₁ + ω₂ + …+ ω_n =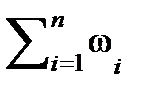

Соответственно, значение среднего времени безотказной работы

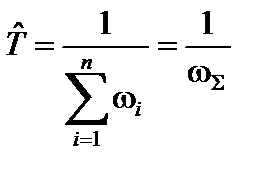(1.31)

и будет определяться как среднее время наработки на отказ.

Если представить 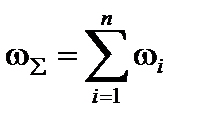как интенсивность отказов системы, сведенной к эквивалентному элементу с интенсивностью отказов 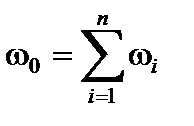= const, то систему из n последовательно включенных элементов легко заменить эквивалентным элементом, который имеет экспоненциальный закон распределения вероятности безотказной работы. А это значит, если ω_o = const, то средняя наработка на отказ системы 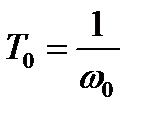. Верно также и то, что при условии ω_o= const, искомая величина определится как .

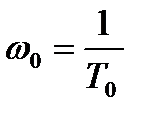Средняя наработка на отказ системы определяется по выражению:

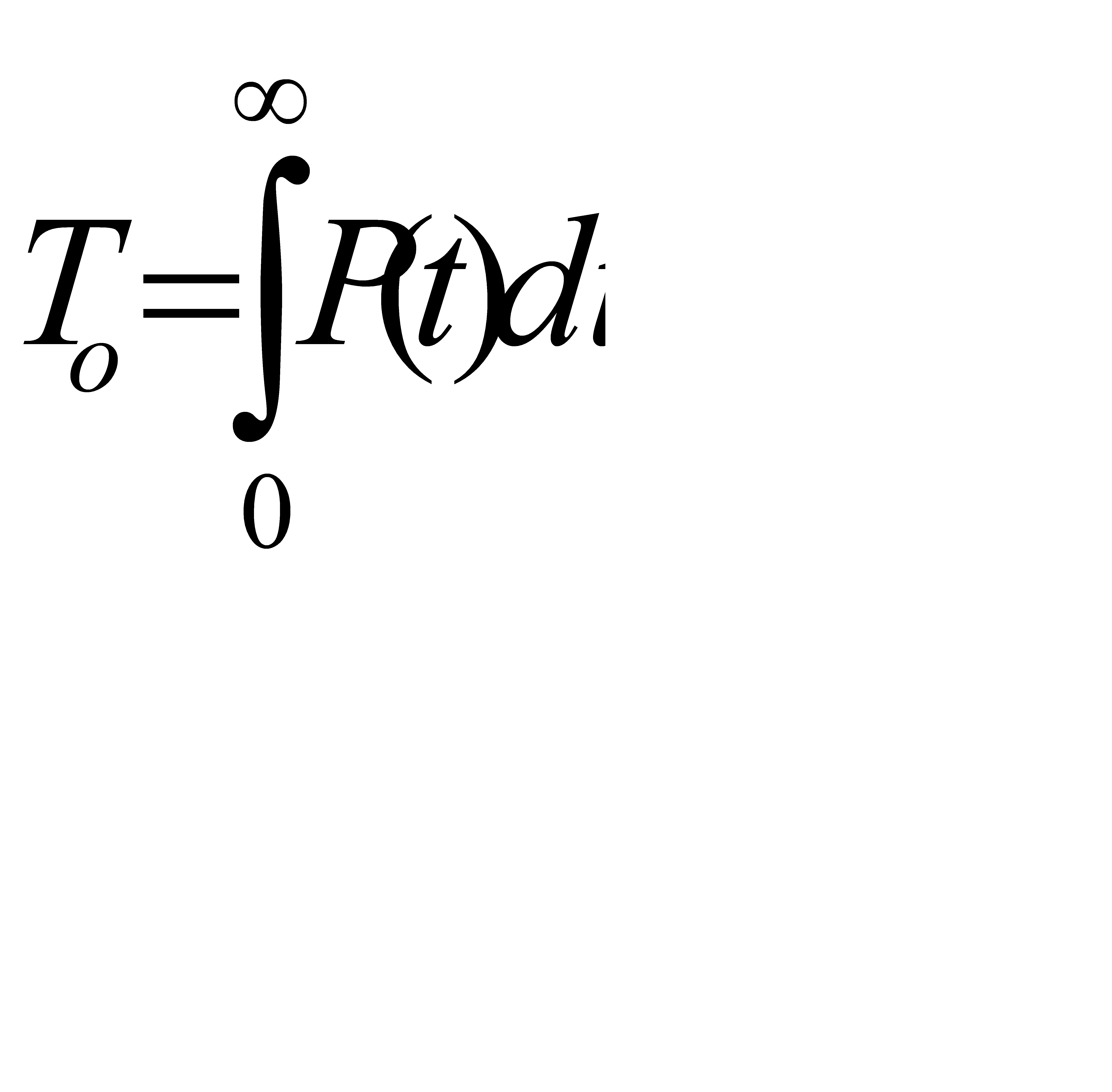(1.32)

Если ω(t) зависит от времени, то при произвольном законе распределения времени, наработка на отказ для каждого из элементов равна:

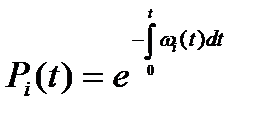, (1.33)

где ω_i(t) - интенсивность отказов i-го элемента.

Вероятность безотказной работы системы соответственно определяется как

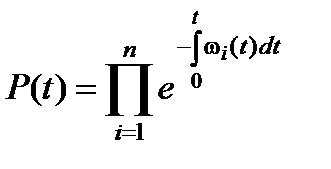(1.34)

По выражению (1.34) можно определить вероятность безотказной работы системы до первого отказа при любом законе изменения интенсивности отказов каждого из n элементов во времени.