Единичные показатели для невосстанавливаемых объектов

Свойство безотказности невосстанавливаемых объектов характеризуют показатели: вероятность безотказной работы, вероятность отказов, интенсивность отказов, время наработки до отказа.

Вероятность безотказной работы - это вероятность того, что время работы объекта до отказа t₀ будет не меньше заданного времени t.

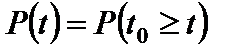. (1.2)

Можно воспользоваться определением вероятности безотказной работы исходя из статистических данных, выявленных во время испытания на вероятность безотказной работы.

Вероятность безотказной работы - это вероятность того, что в пределах заданной наработки отказ объекта не возникает. На практике этот показатель можно определить статистической оценкой.

Вероятность безотказной работы в течение времени t – вероятность того, что за время t не произойдет ни одного отказа объекта :

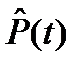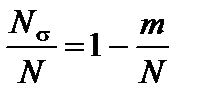= , (1.3)

где 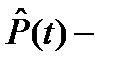среднестатистическое значение вероятности безотказной работы;

m – число элементов ЭУ, отказавших за время t;

N_σ - число однотипных элементов безотказно проработавших до момента времени t;

N – число элементов, работоспособных в начальный момент времени.

Иногда целесообразно пользоваться не вероятностью безотказной работы, а вероятностью отказа Q(t). Поскольку работоспособность и отказ являются состояниями несовместными и противоположными, то их вероятности связаны зависимостью:

Р(t) + Q(t) = 1. (1.4)

Следовательно

Q(t) = 1 - Р(t) . (1.5)

В практических расчетах (для невосстанавливаемых элементов) часто используется другой показатель безотказности - интенсивность отказов λ(t) (плотность условной вероятности отказа).

Определяющая вероятность того, что элемент, проработавший безотказно до момента времени t, откажет в следующей момент (t+Δt) называется плотностью условной вероятности отказа в момент времени t (при условии, что до этого момента изделие работало безотказно) и определяется как:

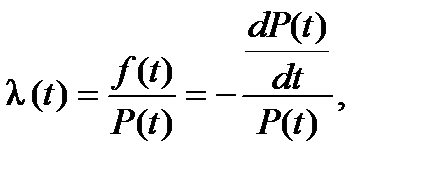(1.6)

где f(t) – плотность распределения наработки до отказа;

Р(t) – вероятность безотказной работы.

Статистическая оценка интенсивности отказов имеет вид:

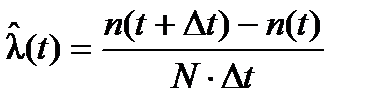, (1.7)

где n(t+Δt), n(t) – число объектов, отказавших на отрезке времени, соответственно, от 0 до (t+Δt) и от 0 до t;

Δt – интервал времени, для которого определяется λ;

N - число однотипных объектов, работающих в начальный момент времени.

Если при статистической оценке среднего значения интенсивности отказов ( 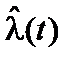) время эксперимента разбить на достаточно большое количество одинаковых интервалов Δt за длительный срок, то результатом обработки опытных данных будет график, изображенный на рис. 1.1.

Как показывают многочисленные данные анализа надежности большинства объектов техники, в том числе и электроустановок, линеаризованная обобщенная зависимость λ(t) представляет собой сложную кривую с тремя характерными интервалами (I, II, III).

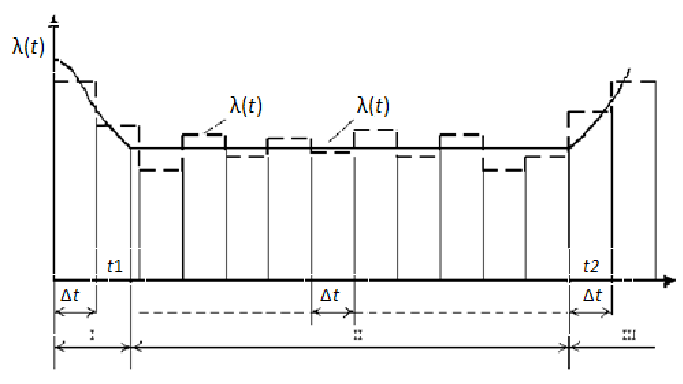
Рис.1.1. Кривая жизни элемента (опытные данные)

Участок (интервал) I соответствует периоду приработки или наладки (обычно непродолжительному). Интервал может увеличиваться или уменьшаться в зависимости от уровня организации отбраковки элементов на заводе-изготовителе, где элементы с внутренними дефектами своевременно изымаются из партии выпускаемой продукции. Величина интенсивности отказов на этом интервале во многом зависит от качества сборки схем сложных устройств, соблюдения требований монтажа и т.п. Включение под нагрузку собранных схем приводит к быстрому "выжиганию" дефектных элементов и по истечении некоторого времени t₁ в схеме остаются только исправные элементы, и их эксплуатация связана с периодом времени, когда λ = const (участок II). Участок II - период нормальной эксплуатации и III участок – участок старения изделия, когда параметр потока отказов возрастает за счет износа, старения изоляции и т.д. На интервале III по причинам, обусловленным естественными процессами старения (изнашивания, коррозии и т.д.), интенсивность отказов резко возрастает, увеличивается число деградационных отказов.

Интервал λ= const соответствует экспоненциальной модели распределения вероятности безотказной работы. Расчеты обычно ведутся для периода нормальной эксплуатации (участок II), когда интенсивность отказов не изменяется длительное время (λ(t) = λ = const).

Поток отказов, имеющий место в течение периода времени II обладает свойствами ординарности, стационарности и отсутствием последствий.

Ординарность заключается в малой вероятности совпадений отказов, которой можно пренебречь

Свойство стационарности выражается в постоянстве параметра потока отказов.

Отсутствие последствия заключается в том, что число отказов в один период времени не зависит от числа отказов в предыдущие.

Такой поток в теории надежности называется простейшим.

Каждый элемент системы с течением времени становится менее надежным. Скорость изменения надежности элемента с течением времени, отнесенная к вероятности безотказной работы в данный момент времени и будет определять интенсивность или опасность отказов. Поэтому зависимость между Р(t) и λ(t) можно записать как:

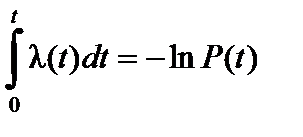или 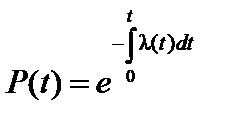, (1.8)

при λ= соnst (принятое выше допущение), формула (1.8) примет вид:

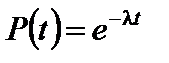. (1.9)

Важной характеристикой надежности является наработка на отказ (время безотказной работы), которое определяется:

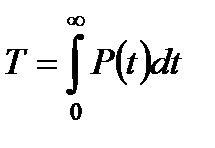. (1.10)

С учетом, что 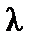= соnst, средняя наработка на отказ равна:

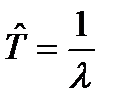. (1.11)

Статистическая оценка для средней наработки на отказ определяется по формуле:

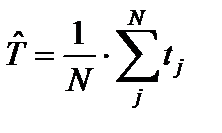, (1.12)

где N – число работоспособных однотипных невосстанавливаемых объектов при t = 0 (в начале испытания);

t_j - наработка на отказ j-го объекта.

Средняя наработка на отказ может оцениваться не только в часах (годах), но и в циклах, километрах пробега и другими аргументами.