Общая и основная задачи линейного программирования
К математическим задачам линейного программирования приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов (задача о раскрое, смесях и т.д.).
Во всех этих задачах требуется найти максимум или минимум линейной функции при условии, что ее переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные неравенства, так и линейные уравнения. Каждая из этиx задач является частным случаем общей задачи линейного программирования.
þ Oбщей задачей линейного программирования называется задача, которая coстоит в определении максимального (минимального) значения функции:
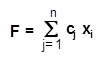 (5.1)
(5.1)
при условии:
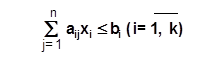 (5.2)
(5.2)
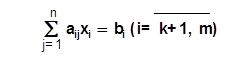 (5.3)
(5.3)
Xj ³ 0 (j=1, 1; 1 £ n) (5.4)
где aij, bi, сj - заданные постоянные величины и k £ m.
þ Функция (5.1) называется целевой функцией (или линейной формой) задачи (5.1)-(5.4), а условия (5.2)-(5.4) - ограничениями данной задачи.
þ Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (5.1) при выполнении условий (5.2) и (5.4), где k=m и 1=n.
þ Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (5.1) при выполнении условий (5.3) и (5.4), где k=0 и 1=n.
þ Совокупность чисел Х* = (x1, x2, ..., xn), удовлетворяющих ограничениям задачи (5.2)-(5.4), называется допустимым решением (или планом).
þ План Х* = (x1, x2, ..., xn), при котором целевая функция задачи (5.1) принимает свое максимальное (минимальное) значение, называется оптимальным.
значение целевой функции (5.1) при плане X будем обозначать через F(X). Следовательно, Х* - оптимальный план задачи, если для любого X выполняется неравенство F(X) £ F(Х*) (соответственно F(X) ³ F(Х*)).
Дата добавления: 2021-09-25; просмотров: 602;











