Принцип Даламбера для СМТ в двух формах

Рассмотрим СМТ, состоящую из МТ с массами m₁, m₂,…, m_n. Выделим какую-нибудь из МТ этой СМТ с массой m_n и обозначим равнодействующую всех приложенных к ней внешних сил через 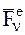, а равнодействующую всех внутренних сил, приложенных к ней же, через 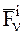. Обозначив через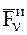 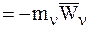– силу инерции, на основании принципа Даламбера для МТ – соотношение (1.49) для всех МТ рассматриваемой СМТ, будем иметь:

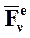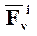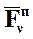+ + = 0 (n = 1,2,…,n). (5.1)

Принцип Даламбера для СМТ:

Действующие на каждую МТ движущейся СМТ внешние и внутренние силы можно в любой момент времени уравновесить добавлением к ним силы инерции.

Из системы равенств (5.1) можно получить принцип Даламбера для СМТ в другом виде. Просуммируем равенства (5.1) по n точкам СМТ:

.

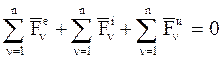Первое слагаемое этого соотношения представляет собой главный вектор всех внешних сил, а второе слагаемое – главный вектор всех внутренних сил:

,

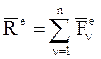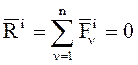
(главный вектор внутренних сил равен нулю на основании свойства внутренних сил – соотношение (3.2)),

а третье слагаемое – главный вектор всех сил инерции:

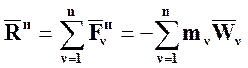. (5.2)

Окончательно получим:

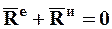. (5.3)

Выбрав в качестве полюса точку О, умножим обе части n-го равенства (5.1) слева векторно на радиус-вектор 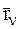, определяющий положение n – й МТ относительно этого полюса, и просуммируем полученное выражение по n точкам СМТ:

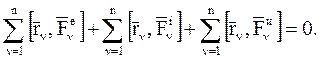
С учетом формулы для момента силы относительно точки (Ч.2 Статика) это выражение примет вид:

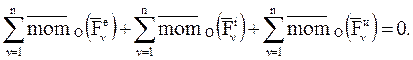
Первое слагаемое равенства представляет собой главный момент внешних сил относительно центра О:

,

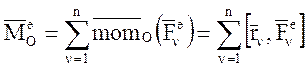второе слагаемое – главный момент всех внутренних сил относительно центра О:

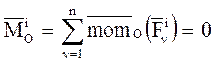
(главный момент всех внутренних сил относительно центра О равен нулю на основании свойства внутренних сил – соотношение (3.3)),

а третье слагаемое – главный момент всех сил инерции относительно того же центра О:

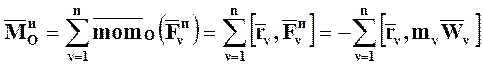. (5.4)

Окончательно получаем

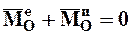. (5.5)

Принцип Даламбера для СМТ: Главный вектор всех внешних сил, действующих на движущуюся СМТ, можно в любой момент уравновесить главным вектором всех сил инерции, а главный момент всех внешних сил, действующих на движущуюся СМТ, относительно какого-либо центра можно в любой момент уравновесить главным моментом всех сил инерции относительно того же центра – соотношения (5.3) и (5.5).

Уравнения (5.3) и (5.5) по форме совпадают с условиями равновесия произвольной системы сил в статике. Однако, в отличие от статики, при выполнении этих уравнений СМТ в состоянии относительного покоя находиться не будет.

Таким образом, принцип Даламбера для СМТ, как и для МТ, дает возможность составлять уравнения движения СМТ в форме уравнений равновесия, вводя в рассмотрение силы инерции. Принцип Даламбера оказывается особенно полезным при решении тех задач динамики, где требуется найти динамические реакции связи, т. е. реакции, возникающие при движении СМТ.

Проектируя соотношения (5.3) и (5.5) на оси декартовой системы координат, можно получить шесть уравнений динамического равновесия.