Лекция № 6. Закон сохранения импульса

Цель: изучить закон сохранения импульса.

Основные понятия:

Механическая система – совокупность взаимодействующих между собой материальных точек (тел).

Внутренние силы – силы взаимодействия между телами данной системы.

Внешние силы – силы воздействия на тела данной системы со стороны тел, не входящих в эту систему.

Замкнутая система – это система тел, на каждое из которых либо не действуют внешние силы, либо действие внешних сил скомпенсировано.

Законы динамики дают возможность полностью описать механическое поведение изучаемой системы, если известны силы, действующие на образующие эту систему материальные точки. Применение второго закона Ньютона к каждой из материальных точек позволяет найти ее ускорение в данном месте в данный момент времени и тем самым последовательно, шаг за шагом, проследить ее движение.

Но часто такая детальная информация о движении бывает не нужна. Иногда нас интересует только конечное состояние изучаемой системы, а ее промежуточные состояния, через которые система проходит в конечное состояние, не представляют интереса. В некоторых случаях нас вообще интересует только движение системы как целого, а не движение отдельных частиц, входящих в систему. В подобных случаях быстрее всего к цели приводит не непосредственное применение законов Ньютона, а использование законов сохранения.

Рассмотрим систему, состоящую из двух тел, например двух звезд.

Силы взаимодействия между телами, входящими в систему (между звездами), называются внутренними силами. Внутренние силы будем обозначать символом 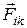. Здесь первый индекс i обозначает номер тела, на которое действует сила 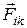, а второй индекс k – номер тела, со стороны которого действует сила .

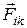По третьему закону Ньютона:

.

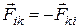Силы воздействия на тела данной системы (две звезды) со стороны тел, не входящих в эту систему (например, соседние космические тела), называются внешними силами.

Равнодействующую всех внешних сил, действующих на i-е тело системы, будем обозначать .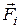

Для каждого тела, входящего в систему, запишем второй закон Ньютона:

,

.

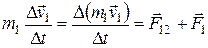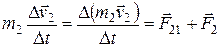Сложив левые и правые части уравнений, получим

.

Учитывая, что 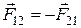, имеем

,

,

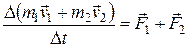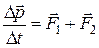где – суммарный импульс системы двух тел.

Из последнего соотношения следует, что изменение суммарного импульса системы тел определяется векторной суммой внешних сил, действующих на эту систему.

Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.

Замкнутая система – это система тел, на каждое из которых либо не действуют внешние силы, либо действие внешних сил скомпенсировано.

Если система тел замкнута, то сумма всех внешних сил, действующих на систему тел, равна нулю, т. е.

.

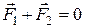Тогда

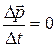, или .

Таким образом, независимо от продолжительности интервала времени импульс системы тел в начале и конце этого интервала времени будет один и тот же, следовательно, 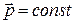или

.

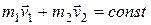Данное соотношение выражает закон сохранения импульса: суммарный импульс замкнутой системы тел с течением времени не изменяется (сохраняется).

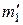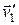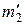Закон сохранения импульса можно записать и в другом виде. Пусть в момент времени t первое тело имеет массу m­₁ и скорость ; второе массу m₂­ и скорость ; в момент времени t¢ - соответственно и , и 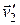. Закон сохранения импульса тогда можно записать в виде:

.

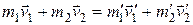Если массы тел с течением времени не изменяются, т. е. , , 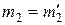то закон сохранения импульса примет вид:

.

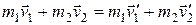Если замкнутая система состоит из нескольких тел, то для нее закон сохранения импульса запишется так:

.

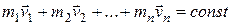Вопросы для самоконтроля:

1. Что называется механической системой?

2. Какие силы называются внутренними, внешними?

3. Какая система тел называется замкнутой? Приведите примеры замкнутых систем тел.

4. Сформулируйте закон сохранения импульса.

5. Запишите закон сохранения импульса для случая, когда массы тел в системе изменяются.

6. Запишите закон сохранения импульса для случая, когда массы тел в системе не изменяются.