Синтез корректирующих устройств САУ методом ЛАЧХ.
Синтез корректирующих устройств методом ЛАЧХ основан на знании желаемой ЛАЧХ проектируемой САУ в разомкнутом состоянии. ЛФЧХ при этом не рассматривается, так как система предполагается минимально-фазовой и при известной ЛАЧХ фазовая характеристика является заданной.
Желаемой ЛАЧХ называется такая ЛАЧХ, которой соответствует система с требуемыми показателями качества (время регулирования tр, перерегулирование s%, установившаяся ошибка еуст). Задачей синтеза корректирующего устройства является выбор его структуры и параметров так, чтобы максимально приблизить ЛАЧХ скорректированной системы к желаемой.
В качестве желаемых часто выбирают так называемые оптимальные характеристики, являющиеся наилучшими в каком-либо смысле. Системы с такими характеристиками называют оптимальными.
Передаточная функция и частотная характеристика оптимальной системы.
При построении желаемых ЛАЧХ разомкнутой системы используется понятие оптимальной системы. Для каждой САУ можно выбрать свои условия оптимальности. Здесь назовем процесс регулирования при ступенчатом задающем воздействии оптимальным, если он является монотонным и время регулирования tр является минимальным при ограниченной второй производной входной величины x(t).
Обозначим 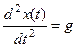 .
.
Время переходного процесса оптимальной системы обозначим через tmin.
Процесс регулирования будет оптимальным, если ускорение g имеет максимальное значение gm и меняет знак при 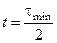 , т.е.
, т.е.
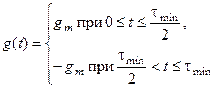
Тогда 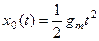 при
при 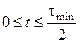 (127)
(127)
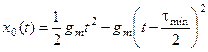 при
при 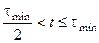 (128)
(128)
x0(t) – управляемая величина в оптимальном процессе.
При 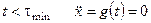 и тогда для
и тогда для 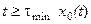 можно записать в виде
можно записать в виде
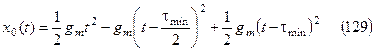
Объединяя (1)-(3) с помощью единичных ступенчатых функций, получим
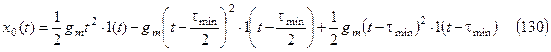
Из зависимости (130) можно получить
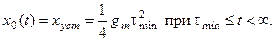
Будем считать, что система воспроизводит ступенчатый сигнал без ошибки, т.е.
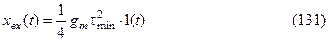
В зависимости от величины входного воздействия будем изменять 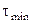
Пусть 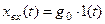 .
.
Тогда 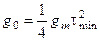 ,
,
откуда 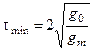 ,
,
это минимальное время отработки ступенчатого сигнала g0 с ускорением управляемой величины, не превосходящем gm.
Найдем передаточную функцию замкнутой оптимальной системы
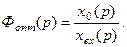 Учитывая (130), (131), получим
Учитывая (130), (131), получим
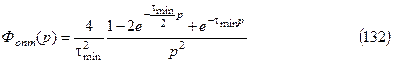
Определим передаточную функцию разомкнутой системы. Имеем
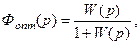
откуда 
и тогда из (132) и (133) найдем
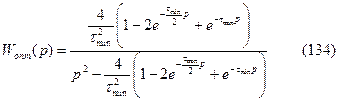
Полученная передаточная функция является трансцендентной функцией p. Это означает, что принятая форма оптимального процесса регулирования, определяемая выражением (130) не может быть точно реализована линейной стационарной САУ. Однако она определяет тот предел, к которому следует приближать процессы в линейной системе с постоянными параметрами.
Зависимость (134) позволяет определить ЛАЧХ оптимальной САУ:
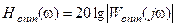 .
.
Из (134) можно найти 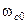 - частоту среза оптимальной системы, такую, что
- частоту среза оптимальной системы, такую, что 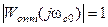 . Имеем
. Имеем
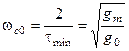 .
.
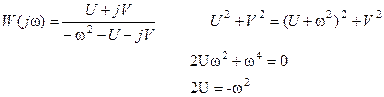
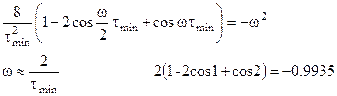
Наклон ЛАЧХ при 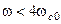 равен –20 дб/дек. Чем ближе будут ЛАЧХ проектируемой САУ к ЛАЧХ оптимальной системы, тем ближе будет проектируемая система к оптимальному варианту.
равен –20 дб/дек. Чем ближе будут ЛАЧХ проектируемой САУ к ЛАЧХ оптимальной системы, тем ближе будет проектируемая система к оптимальному варианту.
| <== предыдущая лекция | | | следующая лекция ==> |
| Синтез линейных стационарных систем автоматического управления (продолжение). | | | Построение желаемой ЛАЧХ. |
Дата добавления: 2017-10-04; просмотров: 2690;











