Методы построения процесса регулирования.

Для определения установившейся ошибки, характеризующей точность системы не нужно строить весь процесс регулирования. Однако обычно кроме точности проектировщика интересует и вид процесса регулирования (колебательный или апериодический) и такие показатели, как перерегулирование и время перерегулирования. Эти показатели можно определить, только построив график всего процесса 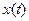( 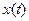-управляемая величина).

Рассмотрим возможные способы построения процесса регулирования 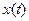в системе, структурная схема которой показана на рисунке 83.

Рис.83

Здесь 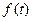-входной сигнал, 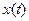-выходной сигнал, 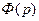-передаточная функция САУ (безразлично, замкнутой или разомкнутой).

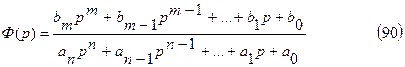
К такой рабочей схеме может быть сведена любая задача определения процесса регулирования в линейной системе.

Передаточной функции Ф(р) соответствует дифференциальное уравнение

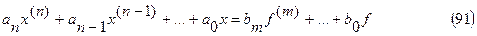
Рассмотрим аналитические способы построения процесса регулирования. В общем случае построение процесса регулирования сводится к решению дифференциального уравнения (91). При нулевых начальных условиях справа, когда

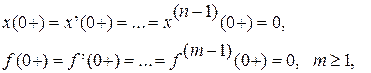
от уравнения (91) можно перейти к уравнению в изображениях

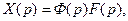
после чего

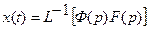
Вычисление обратного преобразования Лапласа было рассмотрено ранее в разделе “Свободный и вынужденный режим движения САУ”.

Пример. Найдем переходную функцию апериодического звена. Уравнение звена имеет вид

При 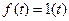последовательно имеем:

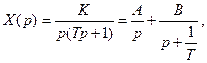
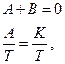
откуда

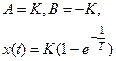
Если начальные условия по переменным 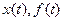известны и они не являются нулевыми, решение уравнения (91) производится с помощью преобразования Лапласа с использованием теоремы об изображении производной (см. тот же раздел – определение свободной составляющей процесса регулирования и рассмотренный там пример).

Пример. В предыдущем уравнении 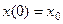. Найти решение уравнения. Применяя преобразование Лапласа к обеим частям уравнения (92) с использованием теоремы об изображении производной, получим

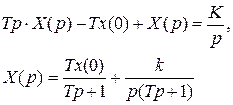
и

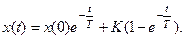
Если известны начальные условия слева 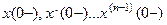и функция 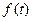такова, что правая часть уравнения (91) при 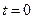имеет разрыв второго рода, то функция 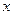и ее производные при 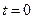могут иметь разрывы первого или второго рода, так что начальные условия справа будут отличаться от начальных условий слева. В этом случае для решения уравнения (92) может использоваться преобразование Лапласа, в котором при вычислении изображений производных используются начальные условия слева, т.е. при x=(0-). После полученного таким образом изображения процесс 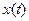находится вычислением обратного преобразования Лапласа

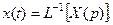
Подробно об этой особенности отдельных САУ было сказано в разделе “Решение дифференциальных уравнений линейных стационарных САУ”.

В частном случае ступенчатого входного сигнала для расчета процесса 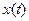могут использоваться частотные характеристики системы.

Частотный метод построения процесса регулирования.

Пусть система устойчива, т.е. корни характеристического уравнения

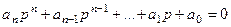
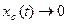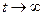левые. В этом случае собственные движения системы при и процесс 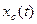является преобразуемой по Фурье функцией. Пусть известно преобразование Фурье 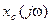собственных движений системы. Найдем .

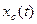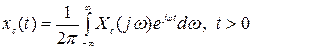
-это формула обратного преобразования Фурье.

Пусть 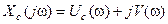, тогда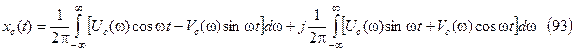

В (93) подынтегральное выражение второго интеграла 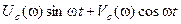- нечетная функция w и так как интеграл вычисляется по центрально-симметричному интервалу, то

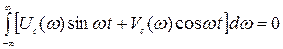и, следовательно

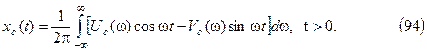
Так как 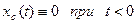,то

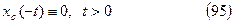
Тогда из (94) с учетом (95) найдем

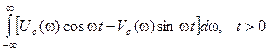
откуда следует, что

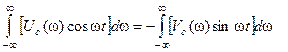
С учетом последнего равенства зависимость (94) можно записать в виде

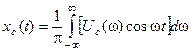
или

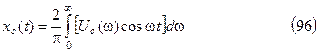
Зависимость для собственного движения системы может быть также приведена к виду

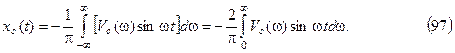
Рассмотрим частный случай, когда и начальные условия нулевые. В этом случае

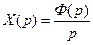- это преобразование Лапласа общего процесса системы и

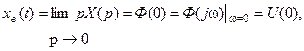
где U(ω) – вещественная ЧХ замкнутой системы. Тогда

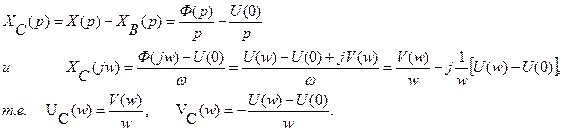
Подставляя выражения для V_c(w) в формулу (97), получим

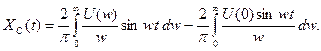(98)

Имеем

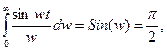
после чего формула (98) может быть приведена к виду

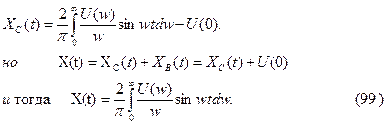
Для процесса x(t) может быть получена и другая формула

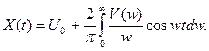
На основе полученных зависимостей разработан графоаналитический способ расчета процесса x(t) c помощью так называемых трапецеидальных вещественных ЧХ . С распространением ЭВМ этот метод утратил свое значение . Однако зависимость (99) указывает на связь между ВЧХ и процессом X(t) и позволяет получить некоторые косвенные оценки процесса регулирования.