ОРТОГОНАЛЬНАЯ СИСТЕМА ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Две проекции точки вполне определяют ее положение в пространстве. Так как каждая фигура или тело представляют собой совокупность точек, то можно утверждать, что две ортогональные проекции предмета вполне определяют его форму.
Однако на практике часто возникает необходимость создания дополнительных проекций. 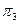 - профильная плоскость проекции [AA3 ]
- профильная плоскость проекции [AA3 ] 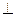
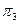 (рис.10).
(рис.10).
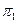
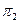
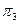
| 
|
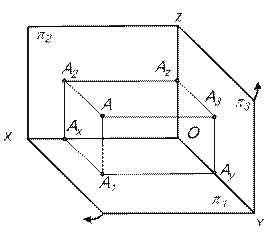
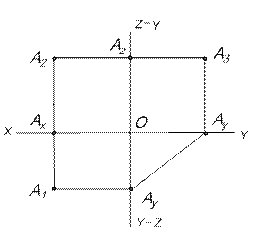
| Рис. 10 |
Проекции точек на профильную плоскость проекций называются профильными проекциями – А3.
Плоскости проекций попарно пересекаясь определяют три оси ОX; ОY и ОZ, которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке О.
А1Ау = Х – абсцисса (расстояние от точки до 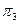 )
)
А1Ах= Y - ординат (расстояние от точки до 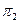 )
)
А2Ах = Z - аппликата (расстояние от точки до 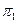 )
)
Длины проецирующих перпендикуляров, определяющих расстояние точки до плоскостей проекций, являются координатами точки. Задание точки осуществляется в следующем виде: А (Х, Y, Z). Знаки координат Х, Y, Z в четырех угловых пространствах показаны в таблице1.
Таблица 1
| X | Y | Z | |
| I | + | + | + |
| II | + | - | + |
| III | + | - | - |
| IV | + | + | - |
1.5. БИССЕКТОРНЫЕ ПЛОСКОСТИ (ПЛОСКОСТЬ СИММЕТРИИ И ПЛОСКОСТЬ ТОЖДЕСТВА)
Плоскость, которая проходит через I и III угловые пространства и делит их пополам, называется плоскостью симметрии и обозначается 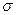 (рис. 11).
(рис. 11).
Плоскость, которая проходит через II и IV угловые пространства и делит их пополам, называется плоскостью тождества и обозначается 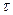 (рис.12).
(рис.12).
| 
|
| Рис. 11 | Рис. 12. |
|
|
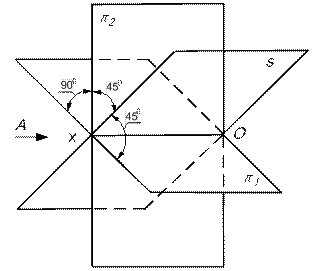
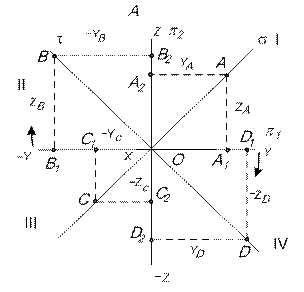
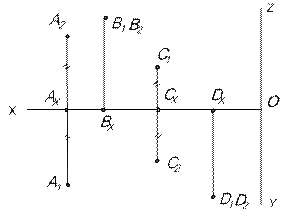
| Рис.13.. |
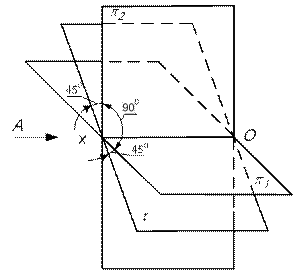
На рис.13 изображен вид А пересекающихся плоскостей 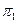 ;
; 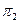 ; s;
; s; 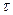 , на котором легко определяются координаты точек A, B, C, D, принадлежащих плоскостям s и
, на котором легко определяются координаты точек A, B, C, D, принадлежащих плоскостям s и 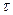 .
.
Координаты Y и Z точек, лежащих на плоскости симметрии одинаковы по величине и по знаку: Уа = ZА ; -УС = ZС.
Координаты Y и Z точек, лежащих на плоскости тождества одинаковы по величине, но противоположны по знаку: -УВ = ZВ; УD = - ZD
1.6.ТОЧКИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО БИССЕКТОРНЫХ ПЛОСКОСТЕЙ.
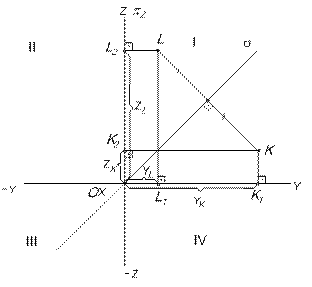
Пусть точка L симметрична точке К относительно s (рис.14). Тогда координата YК равна по величине и по знаку координате ZL (YК = ZL), а координата ZК равна по величине и по знаку координате YL (ZК = YL).
Координаты Y и Z точек, симметричных относительно плоскости симметрии, равны по величине и по знаку координатам Z и Y заданных точек.
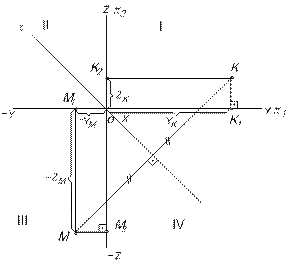
Пусть точка М симметрична точке К относительно плоскости тождества 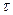 (рис.15). Тогда координаты YК равны по величине, но противоположны по знаку координате –ZМ, а координата ZК равна по величине, но противоположна по знаку координате –YМ (YК = –ZМ; ZК = –YМ).
(рис.15). Тогда координаты YК равны по величине, но противоположны по знаку координате –ZМ, а координата ZК равна по величине, но противоположна по знаку координате –YМ (YК = –ZМ; ZК = –YМ).
| А | А |
| 
|
| Рис.14 | Рис. 15. |
1.8.ТОЧКИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
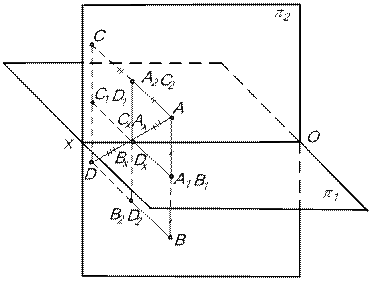
Пусть точка В симметрична точке А относительно плоскости 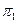 (рис.16).
(рис.16).
|
| Рис.16 |
У точек симметричных относительно горизонтальной плоскости проекций 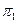 координата Z меняет знак на противоположный ZА= -ZВ. А(Х,Y,Z); В(Х,Y,-Z).
координата Z меняет знак на противоположный ZА= -ZВ. А(Х,Y,Z); В(Х,Y,-Z).
Пусть точка С симметрична точке А относительно плоскости проекций 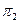 . У точек, симметричных относительно фронтальной плоскости проекций
. У точек, симметричных относительно фронтальной плоскости проекций 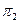 координата Y меняет знак на противоположный -YC= YA. А(Х,Y,Z); С(Х,-Y,Z).
координата Y меняет знак на противоположный -YC= YA. А(Х,Y,Z); С(Х,-Y,Z).
Пусть точка D симметрична точке А относительно оси проекций ОХ. У точек, симметричных относительно оси проекций ОХ, координаты Y и Z меняют знак на противоположный YD= -YA; ZD= -ZA. А(Х,Y,Z); D(Х,-Y,-Z).
Дата добавления: 2017-10-04; просмотров: 1491;











