Вывод соотношения для критического радиуса пузырька

ТЕПЛООБМЕН ПРИ КИПЕНИИ В БОЛЬШОМ ОБЪЕМЕ

Теплообмен при кипении отличается от конвекции дополнительным переносом массы жидкости и теплоты пузырями из пограничного слоя в объем жидкости. Для возникновения кипения необходим перегрев жидкости относительно температуры насыщения и наличие центров парообразования, которыми могут являться неровности поверхности нагрева, пузырьки воздуха, пылинки. Пузырьки пара образуются на поверхности нагрева, где t_c>t_s.

Кипение, при котором пар образуется в виде отдельных пузырьков, называется пузырьковым кипением. С увеличением теплового потока отдельные пузырьки сливаются, образуя у поверхности нагрева сплошной паровой слой с периодически отрывающимися паровыми пузырями (пленочное кипение).

Высокая интенсивность теплоотдачи при пузырьковом кипении объясняется разрушением пограничного слоя у поверхности нагрева паровыми пузырьками.

Условие существования пузырька определяется уравнением Лапласа:

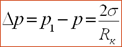(11.1)

согласно которому давление пара р₁ внутри пузырька должно быть выше силы давления жидкости р и силы поверхностного натяжения.

При ∆p>2σ/R_k паровой пузырек растет, а при ∆p<2σ/R_k он сконденсируется.

Критический радиус пузырька можно определить по формуле:

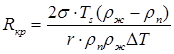
(11.2)

Вывод соотношения для критического радиуса пузырька

Критический радиус пузырька – это тот минимальный радиус, при котором возможно существование паровой фазы при допускаемых термодинамических условиях.

Соотношение для критического радиуса пузырька может быть получено при одновременном рассмотрении законов Лапласа относительно избыточного давления в пузырьке пара и Клапейрона-Клаузиуса.

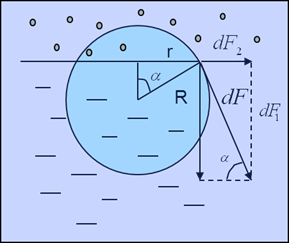
К выводу формулы Лапласа

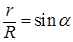
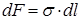
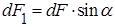
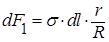
	(11.3)
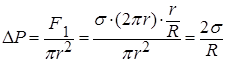
	(11.4)

Таким образом получили соотношение Лапласа:

(11.5)

Давление внутри пузырька больше давления снаружи его на величину ∆Р. Для несферического пузырька закон Лапласа записывается как:

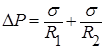
(11.6)