Регулярный режим охлаждения
Анализ решений для охлаждения (нагревания) тел разной формы показывает, что все они представляют сумму бесконечного ряда, члены которого соответствуют быстро убывающим экспоненциальным функциям. где Аn константа для каждого члена ряда, которая находится из начальных условий. Множитель 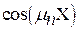 зависит только от координаты Х. Комплекс
зависит только от координаты Х. Комплекс 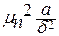 является постоянным, положительным, вещественным числом: m1<m2<…<mn.
является постоянным, положительным, вещественным числом: m1<m2<…<mn.
Тогда уравнение нестационарной теплопроводности запишется в виде:
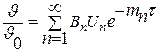 . .
| (4.35) |
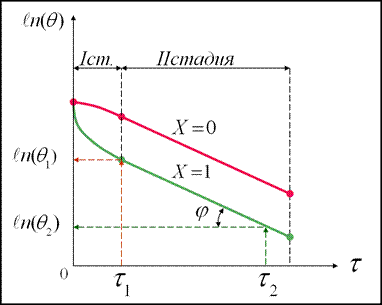
Уравнение справедливо для тел разной геометрии, которая учитывается видом сомножителей An, Un. При малых значениях времени от τ=0 до τ= τ1 изменение температур зависит от начального распределения температур в теле. В этом случае поле температур будет определяться не только первым, но и последующими членами ряда. На рисунке показана «I – неупорядоченная стадия охлаждения».
Регулярный режим охлаждения
Но начиная с некоторого момента времени τ> τ1 начальные условия играют второстепенную роль, процесс определяется интенсивностью охлаждения и физическими свойствами тела.
Тогда температурное поле достаточно точно описывается только первым членом ряда «II стадия охлаждения – регулярный режим», для которого: 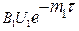 . Логарифмируя этот комплекс и опуская индексы, получим:
. Логарифмируя этот комплекс и опуская индексы, получим:
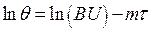 , ,
| (4.36) |
то есть в полулогарифмических координатах эта зависимость прямолинейная. При длительном охлаждении ( τ→∞) все точки тела принимают одинаковую температуру, равную температуре окружающей жидкости. Это III стадия охлаждения – стационарный режим.
Для регулярного режима после дифференцирования предыдущего
уравнения имеем:
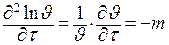 . .
| (4.37) |
то есть относительная скорость изменения температуры равняется константе «m», не зависящей от координат и времени. «m», 1/с – темп охлаждения.
Если есть экспериментальный график изменения избыточной температуры тела во времени, то темп охлаждения в стадии регулярного режима, 1/с:
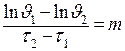 . .
| (4.38) |
Зависимость темпа охлаждения от физических свойств тела, его геометрии, размеров и условий теплообмена на поверхности можно найти из теплового баланса.
Изменение внутренней энергии тела, Дж:
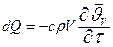 . .
| (4.39) |
где 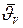 средняя по объему избыточная температура, К.
средняя по объему избыточная температура, К.
Теплота отдается от поверхности тела к окружающей его жидкости. По уравнению конвективной теплоотдачи, Дж:
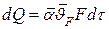 . .
| (4.40) |
Здесь 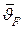 средняя по поверхности избыточная температура;
средняя по поверхности избыточная температура; 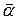 -средний коэффициент теплоотдачи. Приравнивая тепловые потоки с учетом того, что
-средний коэффициент теплоотдачи. Приравнивая тепловые потоки с учетом того, что 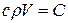 - полная теплоемкость тела, Дж/кг;
- полная теплоемкость тела, Дж/кг; 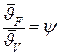 -коэффициент неравномерности распределения температуры в теле, имеем:
-коэффициент неравномерности распределения температуры в теле, имеем:
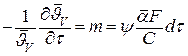 . .
| (4.41) |
то есть при 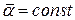 темп охлаждения однородного изотропного тела (относительная скорость охлаждения) пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его полной теплоемкости (первая теорема Кондратьева).
темп охлаждения однородного изотропного тела (относительная скорость охлаждения) пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его полной теплоемкости (первая теорема Кондратьева).
Итак, рассмотрим коэффициент неравномерности распределения температуры в теле входящий в выражения для темпа охлаждения 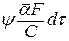 . Как же он зависит от числа Био?
. Как же он зависит от числа Био?
А) Bi →0 (практически Bi < 0,1) – внешняя задача: распределение температур не зависит от геометрических размеров тела и его физических свойств 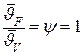 .
.
В) Bi →∞ (практически Bi >100) – внутренняя задача: распределение температур зависит только от геометрических размеров тела и его физических свойств. Из-за высокого внешнего коэффициента теплоотдачи
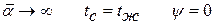 . .
| (4.42) |
Следовательно, в общем случае, коэффициент ψ будет изменяться от (1 при Bi = 0) до (0 при Bi = ∞).
При Bi →∞ (α→∞) темп охлаждения тела «m» становится пропорциональным его коэффициенту температуропроводности a. (вторая теорема Кондратьева):
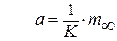 . .
| (4.43) |
Здесь К –коэффициент формы. Он равен для:  пластины
пластины 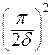 ,
,  цилиндра
цилиндра 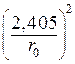 , для параллелепипеда
, для параллелепипеда 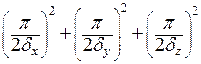 , для цилиндрической болванки
, для цилиндрической болванки 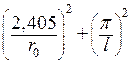 .
.
Дата добавления: 2017-10-04; просмотров: 2613;











