Интерференция на клине.

Если в пространстве распространяются две волны, то в каждой точке результирующее колебание представляет собой геометрическую сумму колебаний, соответствующих каждой из складывающихся волн. Это утверждение называется принципом суперпозиции волн. Принцип суперпозиции волн соблюдается обычно с большой точностью и нарушается только при распространении волн в какой-либо среде, если амплитуда (интенсивность) волн очень велика. Физически содержание принципа суперпозиции для электромагнитных волн означает, что если в среде распространяется несколько электромагнитных волн, то среда реагирует на каждую волну так, как будто других волн нет. Математически это означает, что напряженность электрического поля и индукция магнитного поля в любой точке пространства и в любой момент времени равны соответственно векторной сумме напряженностей и магнитных индукций всех полей в данной точке. К наиболее интересным и красивым явлениям, которые возникают вследствие суперпозиции волн, относятся явления интерференции и дифракции света, являющиеся наиболее яркими проявлениями волновой природы света.

Под интерференцией света понимают широкий круг явлений, в которых при наложении световых пучков результирующая интенсивность в любой точке не равна сумме интенсивностей отдельных пучков. В результате интерференции происходит перераспределение энергии в пространстве: в одних местах интенсивность света больше суммы интенсивностей двух или нескольких волн, в других – меньше. Поэтому интерференционная картина представляет чередование светлых и темных полос. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на мокром асфальте, цвета побежалости на поверхности закаленных металлов радужная окраска мыльных пузырей, Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто.

Условием получения устойчивой картины интерференции является наличие, по крайней мере, двух накладывающихся друг на друга когерентных монохроматических волн, оптическая разность хода которых в точке наблюдения меньше длины когерентности световой волны. Для гармонических складывающих волн условия когерентности можно сформулировать следующим образом: 1)складывающиеся волны должны иметь одинаковые или близкие частоты колебаний; 2) разность фаз складывающихся волн должна быть постоянной во времени; 3) векторы напряженности электрических полей должны быть одинаково направлены.

Известны различные оптические схемы, позволяющие получать эти волны путем деления светового пучка на пространственно разведенные части, рассматриваемые как отдельные световые пучки: это деление фронта волны и деление амплитуды.

Рассмотрим метод деления амплитуд на плоскопараллельной, расположенной в вакууме пленке, ,толщины h с показателем преломления 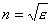, где 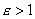- диэлектрическая проницаемость пленки, освещаемой плоской световой монохроматической волной с длиной волны l под углом a.(см.р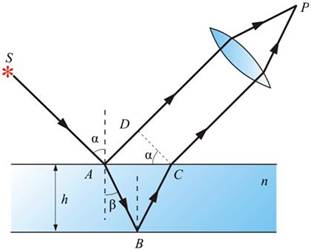ис.2)

Рис.2

В этом случае оба луча, идущие от S к P, порождены одним падающим лучом, и после отражения от верхней и нижней поверхностей пластинки параллельны друг другу.. Часть падающей волны, отраженная от верхней грани пластины,. проходит оптический путь AD. Другая часть волны проходит через пластину (луч AB) и, выйдя из нее, продолжает распространение в направлении первого луча.

Для того, чтобы определить условия для максимумов и минимумов интенсивности картины интерференции этих волн, нам требуется установить зависимость их оптической разности хода D от геометрических параметров рассматриваемой интерференционной схемы, а именно - от угла падения плоской волны на пластину и толщины пластины. Оптическая разность хода между ними в точке P такая же, как на линии DC. являющейся волновой поверхностью

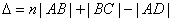. (1)

Предполагается, что над и под пластинкой находится воздух, т.е. n@1. Так как

,

,

,

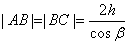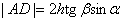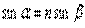для разности хода получаем

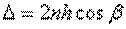. (2)

Следует также учесть, что при отражении волны от верхней поверхности пластинки фаза вектора напряженности электрического поля изменяется на π, так как отражение происходит от более плотной среды. Поэтому разность хода складываемых волн в точке P изменится на l/2 и равна

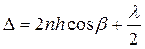(3)

При условии, что

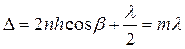(4)

кратно целому числу 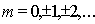... длин волн, в точке наблюдения 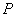на расстоянии от поверхности плёнки во много раз большем, чем толщина пластинки, отражённые от обеих поверхностей пластинки волны будут складываться в фазе и формировать интерференционный максимум.

Аналогичным образом получим условия минимума интерференционной картины в точке наблюдения 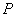на бесконечности, если волны отражённые от обеих поверхностей пластинки волны будут складываться в противофазе, т.е.

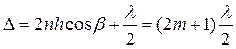(5)

где 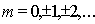произвольное целое число.

Интерференционная картина, образованная отражёнными под разными углами плоскими волнами от поверхностей плоско параллельной пластинки / плёнки, получила название интерференционных полос равного наклона. В этом названии отражается тот факт, что наблюдаемая интерференционная картина образована параллельно распространяющимися волнами, падающими на пластинку под одним углом наклоном. Область наблюдения интерференции расположена в бесконечности, где "пересекаются" параллельные лучи. Углы, в направлении которых формируются максимумы и минимумы интерференционной картины в соответствии с (4.и 5) зависят от длины волны. Это объясняет окраску интерференционной картины световых лучей, отражённых от поверхностей плоско параллельной пластинки при её облучении белым светом.

Полосы равного наклона можно получить не только в отраженном свете, но и в свете, проходящем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая. Постройте ход лучей самостоятельно для проходящего света.

Другой вид интерференции света в тонких плёнках, толщина которых меняется по поперечному сечению, получил название интерференционных полос равной толщины. Для изучения этого явления рассмотрим плёнку переменной толщины в виде клина (рис. 3). Рассмотрим падающую на поверхность диэлектрического клина с показателем преломления 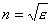, где 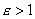- диэлектрическая проницаемость диэлектрика, плоскую световую монохроматическую волну I с длиной волны 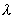(рис. 3).

Отражённые от верхней и нижней граней клина плоские волны (рис. 3) пересекутся вблизи поверхности клина из-за не параллельности его граней . Следовательно, при помещении экрана вблизи поверхности клина можно наблюдать интерференционную картину в виде полос, параллельных ребру клина, которую образуют волны, отразившиеся от его граней в тех точках их поверхности, где клин имеет одинаковую толщину. Это объясняет название рассматриваемого явления.

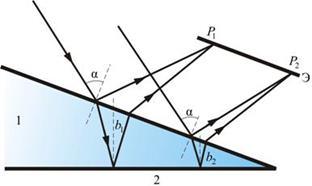Рис.3

Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость). Интерференция будет наблюдаться только во 2-й области клина, так как в

будет больше длины когерентности. Результат интерференции в точках 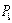и 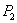экрана определяется по известной формуле

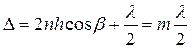, (6)

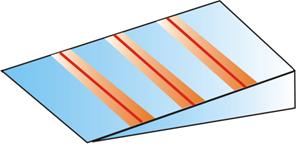Рис.4

подставляя в неё толщину пленки в месте падения луча ( h₁ или h₂). Свет обязательно должен быть параллельным ( 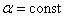): если одновременно , будут. изменяться два параметра h и α, то устойчивой интерференционной картины не. будет. При облучении поверхности клина белым светом интерференционная картина в виде полос равной толщины оказывается окрашенной в цвета оптического спектра.(рис.4)

В случае нормального падения лучей на клин оптическую разность хода определяется по формуле (рис.5)

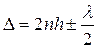
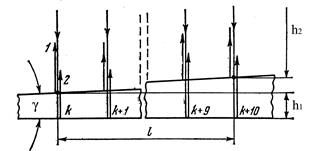Рис. 5

Пусть точкам P₁ и P₂ соответствуют две соседние светлые полосы, тогда

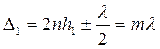
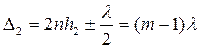
Вычитая , эти два равенства друг из друга, найдем

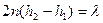
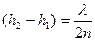
Пусть произвольной темной полоске номера m соответствует определенная толщина клина в этом месте h₁, а темной полоске номера m-1 соответствует толщина клина h₂.

Расстояние между соседними максимумами(см.рис.5)

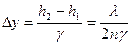(7)

Из формулы (7) видно, что , зная длину волны лазерного излучения l, показатель преломления стекла n и измерив ширину интерференционной полосы Dy, можно определить преломляющий угол клина g.

Для определения преломляющего угла клина g используется установка: микроскоп, клин, расположенный на столике микроскопа, лазер.