Кодовое разделение каналов

Этот метод применяется только в двоичных цифровых СПИ с ФМ. В одноканальной СПИ с ФМ для передачи каждого бита от источника используется радиоимпульс прямоугольной формы, начальная фаза которого определяется значением этого бита, например, 0° при передаче единицы и 180° при передаче нуля. Длительность этого информационного импульса τ_и = 1/V, где V – скорость передачи, бит/с. Ширина спектра такого сигнала примерно равна Δf ≈ 2/τ_и = 2V. При малой скорости передачи сигнал занимает узкую полосу частот.

Для организации кодового разделения каналов в многоканальной СПИ каждый канальный информационный импульс (рис. 20.6а) подвергается дополнительной внутриимпульсной фазовой модуляции (рис. 20.6б).

Для этого импульс разбивается на B частей равной длины (на B более коротких импульсов-чипов).

Для данного канала раз и навсегда задана B-разрядная двоичная последовательность, определяющая закон внутриимпульсной фазовой модуляции, причем элементы этой последовательности удобно обозначить как +1 и –1 вместо традиционных 1 и 0. Далее каждый элемент сигнала умножается на соответствующий элемент последовательности, то есть остается без изменений, если множитель равен +1 и инвертируется в случае –1.

В итоге ширина спектра канального сигнала увеличивается в В раз по сравнению с традиционным методом передачи без внутриимпульсной модуляции, так как теперь сигнал фактически состоит из более коротких импульсов. Кстати, метод внутриимпульсной ФМ является самым распространенным методом искусственного расширения спектра сигнала и часто применяется в других областях радиоэлектроники, например в радиолокации.

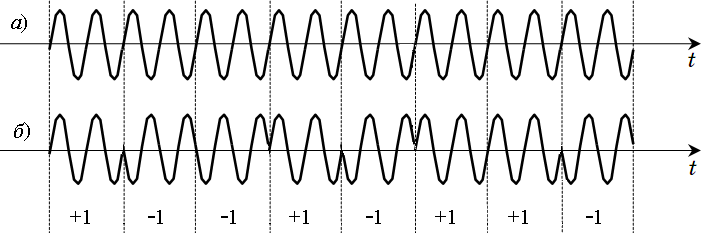
Рис. 20.6. Преобразование информационного импульса в сигнал с внутриимпульсной ФМ:

а – до преобразования; б – после преобразования

Все канальные сигналы передаются одновременно в одной и той же широкой полосе частот. Каждому канальному сигналу присваивается своя двоичная последовательность, определяющая закон внутриимпульсной ФМ, так, чтобы сигналы всех каналов были взаимно ортогональны. Два канальных ФМ сигнала ортогональны, если в двоичных последовательностях, определяющих законы их внутриимпульсной ФМ, число совпадающих элементов равно числу несовпадений. Например, если одному из каналов присвоена последовательность, показанная на рис. 20.6, то другим каналам можно присвоить, допустим, такие последовательности:

+1, –1, +1, –1, –1, +1, –1, +1, …

+1, –1, –1, +1, +1, –1, –1, +1, ...

В системах МДКР операции выделения нужного канального сигнала из суммарного, группового сигнала и демодуляции можно совместить. Для этого можно использовать корреляционный приемник (или заменяющий его согласованный фильтр) и в качестве опорного сигнала использовать целиком импульс с внутриимпульсной ФМ. Таким образом, в системах МДКР устройство разделения каналов и канальные демодуляторы – это набор, состоящий из n корреляционных приемников.

Максимальное число ортогональных последовательностей равно B, следовательно, именно таково количество каналов, работающих без взаимных помех.

Для практического применения подбирают последовательности, обладающие лучшими спектральными свойствами (широкий спектр). Хорошие результаты дает использование отрезков псевдослучайной двоичной последовательности (ПСП).

Так как в системах МДКР не предусматривается взаимная синхронизация каналов, т.е. модулирующие последовательности в разных каналах произвольно сдвинуты во времени, это может привести к нарушению их ортогональности и явиться причиной междуканальных помех.

Метод МДКР используется пока лишь в гражданских и военных системах радиосвязи с подвижными объектами. Следует упомянуть стандарт IS-95, в соответствии с которым построены сотовые системы CDMA и спутниковая система связи с подвижными объектами Globalstar (В = 64, ширина спектра группового и каждого из канальных сигналов равна 1,25 МГц).