ВОПРОС 27. РАСЧЁТ ПРОЧНОСТИ ЗУБЬЕВ ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПРЯМОЗУБОЙ ПЕРЕДАЧИ.

Расчет прочности зубьев по контактным напряжениям

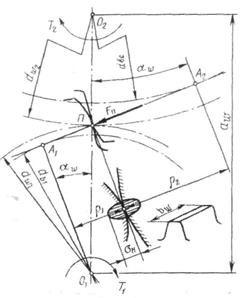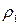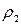Исследованиями установлено, что наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление.. Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления. Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами , и . При этом контактные напряжения определяют по формуле Герца, а именно:

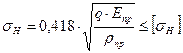
Для прямозубых передач можно записать:

).

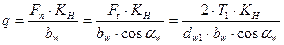
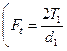
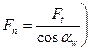Радиусы кривизны эвольвент зубьев в точке контакта (рис. 8.18)

;

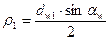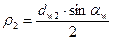
где ,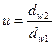

знак « + » ‑ для наружного, а « - » ‑ для внутреннего зацепления.

Подставим два полученных выражения в формулу Герца, получим

(*)

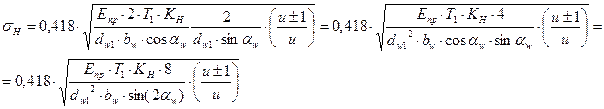
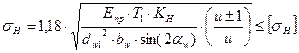Расчет прочности зубьев по напряжениям изгиба

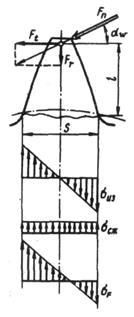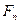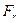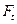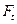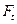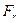Силу переносим по линии действия на ось симметрии зуба и раскладываем на составляющие и . При этом радиус приложения окружной силы будет несколько больше радиуса начальной окружности. Пренебрегая этой разностью, для расчета сил и . Напряжение в опасном сечении, расположенном вблизи хорды основной окружности:

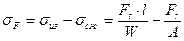
где 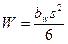‑ момент сопротивления сечения при изгибе;

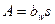‑ площадь;

Знак « - » в формуле указывает, что за расчетные напряжения принимают напряжения на растянутой стороне зуба, так как в большинстве случаев практики именно здесь возникают трещины усталостного разрушения (для стали растяжение опаснее сжатия).

Размеры 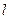и 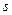неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, их выражают через безразмерные коэффициенты:

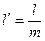и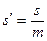

где 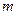‑ модуль зубьев.

После подстановки и введения расчетных коэффициентов получают

где 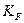‑ коэффициент расчетной нагрузки;

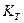‑ теоретический коэффициент концентрации напряжений.

Далее обозначают

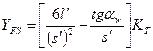‑ коэффициент формы зуба (для наружных зубьев рис. 8.20).

Для колес с внутренними зубьями приближенно можно принимать 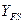= 3,5…4большие величины ‑ при меньших z.

При этом для прямозубых передач расчетную формулу записывают в виде

(**)

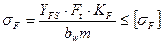где 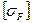‑ допускаемое напряжение изгиба.