Тема 3. Дифракция Фраунгофера

Фраунгофер рассмотрел дифракцию плоских световых волн,илидифракцию в параллельных лучах,которую можнонаблюдать в том случае, если источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием. Если плоская монохроматическая световая волна падает нормально плоскости узкой щелишириной а (рис. 5), то оптическая разность хода D между крайними лучами МС и ND, идущими от щели в произвольном направлении j (j – угол дифракции): .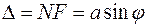

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля. Ширина каждой зоны выбирается так, чтобы разность хода от краевэтих зон была равна l/2, т. е. всего на ширине щели уместится D:l/2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом.

Рис. 5 Следовательно, все точки волнового фронта

в плоскости щели будут колебаться в одинаковой фазе.

Рис. 4

Так как число зон Френеля, укладывающихся на ширине щели, зависит от угла j ,аот числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн, то из приведенного построения (рис. 5) следуют условия наблюдения дифракционного максимума и дифракционного минимума.

Если число зон Френеля, укладывающихся на щели, нечетное, то в точке В наблюдаетсядифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля.

Этому условию соответствует соотношение:

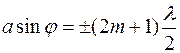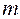( = 1, 2, 3, …) .

Если же число зон Френеля, укладывающихся на щели, четное, то в точке В наблюдаетсядифракционный минимум (при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга). Этому условию соответствует соотношение:

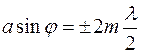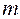( = 1, 2, 3, …) .