Также однозначно определяет структуру графа.
Весьма важным видом графа является связный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путем.
Рассмотрим связный граф 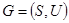 , пусть
, пусть 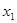 и
и 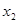 - две его вершины. Длина кратчайшего
- две его вершины. Длина кратчайшего 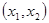 - маршрута называется расстоянием между вершинами
- маршрута называется расстоянием между вершинами 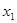 и
и 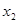 обозначается через
обозначается через 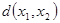 . Очевидно, что расстояние между вершинами является простой цепью и
. Очевидно, что расстояние между вершинами является простой цепью и 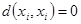 . Для любой вершины
. Для любой вершины 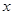 величина
величина
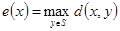 (1.13.6)
(1.13.6)
называется эксцентриситетом вершины 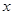 . Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается
. Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается 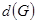 , т. е.
, т. е.
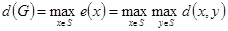 . (1.13.7)
. (1.13.7)
Минимальный из эксцентриситетов вершин графа называется его радиусом и обозначается через 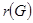 :
:
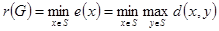 . (1.13.8)
. (1.13.8)
Вершина 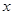 называется периферийной, если ее эксцентриситет равен диаметру графа, т. е.
называется периферийной, если ее эксцентриситет равен диаметру графа, т. е. 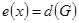 . Простая цепь, расстояние между концами которой равно
. Простая цепь, расстояние между концами которой равно 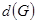 , называется диаметральной цепью.
, называется диаметральной цепью.
Вершина 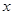 называется центральной, если
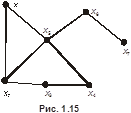
называется центральной, если 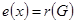 . Множество всех центральных вершин графа называется его центром. Центром может быть единственная вершина графа или несколько вершин (см. рис. 1.15). Здесь
. Множество всех центральных вершин графа называется его центром. Центром может быть единственная вершина графа или несколько вершин (см. рис. 1.15). Здесь 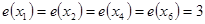 ,
, 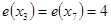 ,
,
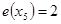 . Таким образом,
. Таким образом, 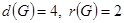 . Периферийные вершины
. Периферийные вершины 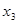 и
и 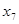 , диаметральные цепи:
, диаметральные цепи: 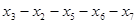 и
и 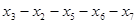 , центральная вершина
, центральная вершина 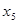 .
.
Дата добавления: 2016-06-05; просмотров: 1529;











