Свойства оператора «лапласиан».

Рассмотрим уравнение:

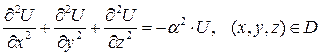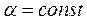, . (41)

Если выполнено условие 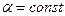, функция 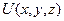является собственной функцией, а величина постоянной 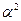является собственным значением оператора «лапласиан». Функция U должна удовлетворять однородным условиям на границе области. Для целей настоящего анализа достаточно рассмотреть граничные условия вида

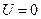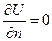или на 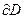. (42)

Математическая задача (41)-(42) имеет специальное название – спектральная задача или задача на собственные значения, при её решении исключается тривиальный случай U=0.

Покажем, что собственными значениями рассматриваемой спектральной задачи являются положительные величины. Это свойство имеет значимое физическое содержание. Перепишем уравнение (41) в символической форме и умножим его левую и правую части на функцию 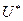, комплексно сопряжённую функции U :

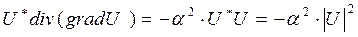. (43)

Воспользуемся известным тождеством векторного анализа

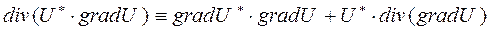(44)

и очевидным соотношением

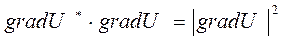. (45)

Перепишем уравнение (43) в форме

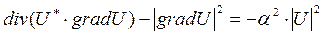. (46)

Далее выполняем интегрирование уравнения (46) по области D. В силу интегральной теоремы Остроградского-Гаусса и рассматриваемых граничных условий (42) первый член левой части уравнения (46) при интегрировании обращается в нуль:

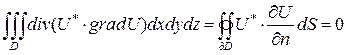. (47)

С учётом полученного результата приходим к соотношению:

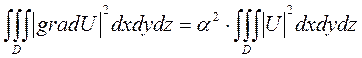. (48)

Приведённые выкладки можно практически дословно повторить и для двумерного случая:

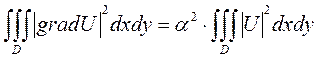, (49)

после чего становится очевидным соотношение

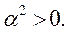(50)

Физическое содержание полученного результата состоит в том, что продольное волновое число должно быть меньше модуля волнового вектора электромагнитной волны в рассматриваемой среде, заполняющей безграничное пространство:

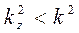
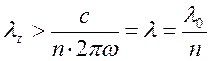. (51)

Следствием этого является утверждение, что длина электромагнитной волны вдоль оси z не может быть меньше вполне определённой величины, т.е. волновод с бесконечно проводящими стенками является фильтром: он пропускает волны одной длины и не пропускает волны другой длины волны. Параметры волновода можно выбрать такими, что волновод будет пропускать только волну одной единственной длины, или не пропускать ни одной из волн. Правда, сделанные выводы основаны на предположении, что собственные значения оператора лапласиана (с граничными условиями (42)) пробегают дискретную последовательность значений. В курсах математической физики доказано, что это справедливо.