Решение уравнения Гельмгольца в прямоугольнике.
Рассмотрим уравнение Гельмгольца в прямоугольной области конечных размеров:
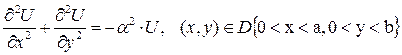 . (49)
. (49)
Следуя методу «разделения переменных», предложенного французским математиком Фурье ещё в 1816 году, ищем решение этого уравнения в форме произведения двух функций (по числу измерений!), каждая из которых зависит только от одной пространственной переменной:
 . (50)
. (50)
Подставим зависимость (50) в уравнение (49) и разделим все члены получаемого соотношения на искомую функцию:
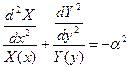 . (51)
. (51)
Поскольку переменные х и у являются независимыми, единственная возможность заключается в предположении, что справедливы уравнения
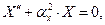

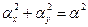 . (52)
. (52)
Общие решения уравнений (52) имеют вид:
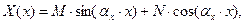
 (53)
(53)
Частные решения уравнения (49) с точностью до произвольного сомножителя представляют собой следующую совокупность комбинаций произведений:
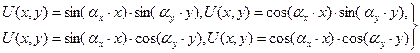 (54)
(54)
Для задачи первого рода с граничным условием U(x,y)=0 на границе области D допустимым решением является последовательность зависимостей
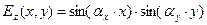 ,
, 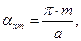

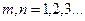 (55)
(55)
На рисунках 3 и 4 показана графическая иллюстрация зависимостей (55) для двух конкретных наборов параметров m и n, размеры прямоугольной области указаны в подписях к рисункам.
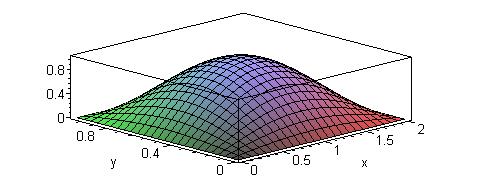
Рис. 3. Продольная компонента электрического поля Ez в поперечном сечении волновода (a=2,b=1,m=1,n=1).
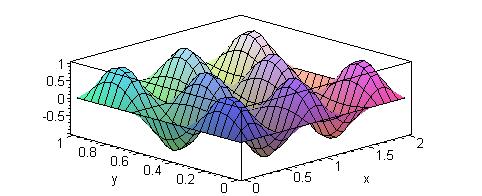
Рис. 4. Продольная компонента электрического поля Ez в поперечном сечении волновода (a=2,b=1,m=5,n=3).
Для краевой задачи второго рода (граничное условие – нормальная производная равна нулю на границе области) из соотношений (54) выбираем последовательность:
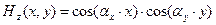 ,
, 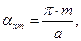

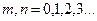 (56)
(56)
На рисунках 5 и 6 показаны трёхмерные графики конкретных членов последовательности (56). Для удобства сравнения результатов решения первой и второй краевой задачи значения индексов m и n на рисунках 3 и 5, а также на рисунках 4 и 6 совпадают.

Рис. 5. Продольная компонента магнитного поля Hz в поперечном сечении волновода (a=2,b=1,m=1,n=1).
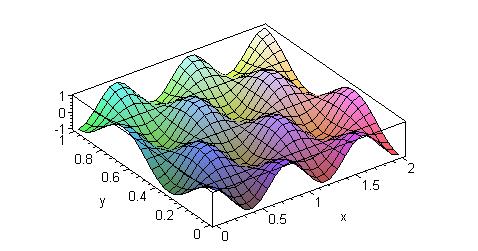
Рис. 6. Продольная компонента электрического поля Hz в поперечном сечении волновода (a=2,b=1,m=5,n=3).
Если интерпретировать приведённые результаты как результаты анализа распространения электромагнитных волн Е-типа и Н-типа в волноводе прямоугольного сечения конечных размеров, необходимо отсечь все комбинации индексов m и n, при которых величина 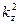 оказывается отрицательной. Для оставшихся допустимых комбинаций индексов можно получить распределения всех проекций векторов напряжённости электрического и магнитного полей по области D с использованием зависимостей (10) или (25), т.е. довести решение задачи до конца.
оказывается отрицательной. Для оставшихся допустимых комбинаций индексов можно получить распределения всех проекций векторов напряжённости электрического и магнитного полей по области D с использованием зависимостей (10) или (25), т.е. довести решение задачи до конца.
Дата добавления: 2017-09-01; просмотров: 3206;










