Распространение электромагнитных волн в волноводах

Эффективная передача сигналов с помощью электромагнитных волн возможна с использованием так называемых направляющих структур. Простейшая направляющая структура – это двухпроводная линия, волновые процессы в которой были описаны в одном из предыдущих разделов. Особенностью волновых процессов в двухпроводной линии является излучение электромагнитной энергии в окружающее пространство, что часто является неприемлемым, особенно при использовании электромагнитных волн высокой частоты. В радиотехнике и технике СВЧ нашли широкое применение волноводы. Волновод представляет собой полую тонкостенную трубку с заданным поперечным сечением. Стенки волновода могут проводить электрический ток, форма и размеры поперечного сечения волновода могут изменяться вдоль оси волновода. Ось волновода может быть пространственной кривой. Основные задачи теории волноводов: какие волны могут распространяться в конкретном волноводе, каким образом возбуждаются электромагнитные волны в волноводе, каким образом происходят переходные процессы в волноводе. Основы теоретического описания распространения электромагнитных волн в волноводе были разработаны в пятидесятые - шестидесятые годы прошлого века, значительный вклад в развитие теории волноводов внесли российские учёные.

Полное описание волновых процессов в рассматриваемых устройствах требует привлечения методов математической физики, а выполнение конкретных расчётов в современных условиях немыслимо без привлечения вычислительной математики и компьютерных технологий. В настоящем пособии рассмотрена проблема определения типов гармонических электромагнитных волн в достаточно длинном прямолинейном волноводе произвольного поперечного сечения с бесконечно проводящими стенками. Для случая волновода с прямоугольным поперечным сечением и волновода с круглым поперечным сечением рассмотрение доведено до конкретных численных результатов, при этом читателю предоставляется возможность освоить логическую последовательность приёмов построения физико-математической модели явления и её анализа.

1. Бегущие гармонические электромагнитные волны в волноводе произвольного поперечного сечения.

Рассмотрим прямолинейный волновод, ось которого направлена вдоль координаты z декартовой системы координат, а поперечное сечение представляет собой односвязную область D(x,y), граница которой 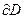является простым достаточно гладким замкнутым контуром. Оговоримся, что будем рассматривать правую систему декартовых координат (x,y,z). Предположим, что вектор напряжённости электрического поля 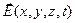и вектор напряжённости магнитного поля 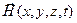внутри волновода могут быть описаны зависимостями

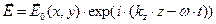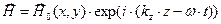, . (1)

Соотношения (1) описывают гармонические волны, бегущие в положительном направлении оси z, амплитуда которых зависит только от поперечных координат точки наблюдения. Величина 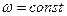является круговой частотой электромагнитной волны, а величина 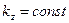- продольным волновым числом, определяющим длину волны 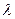в продольном направлении. Заметим, что волны (1) не подпадают под определение «плоская волна», для которой требуется специфическая зависимость амплитуды зависимости (1) от поперечных координат. Заметим также, что ниже рассматриваем проблему «установившихся колебаний», т.е. физическую ситуацию, в которой зависимость исследуемых величин от времени предопределена – гармоническая форма колебаний задана для любого промежутка времени. Последнее значительно упрощает математическую теорию, поскольку позволяет рассматривать «задачу без начальных условий».

В рамках линейной электродинамики, если среда внутри волновода является однородной, изотропной и непроводящей (диэлектрик), процесс распространения электромагнитной волны вида (1) описывается системой уравнений

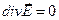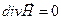, . (2)

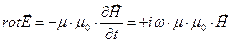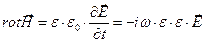, . (3)

Система уравнений (2)-(3) является частым случаем системы уравнений Максвелла, при выводе уравнений (2)-(3) учтен гармонический характер волны. При вычислении результатов пространственных производных в системе уравнений (2)-(3) учтём известные тождества векторного анализа

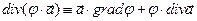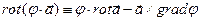, . (4)

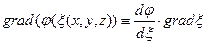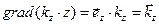, (5)

и то обстоятельство, что амплитуды искомых величин (1) зависят только от поперечных координат. В итоге получаем систему дифференциальных уравнений частных производных в координатной форме:

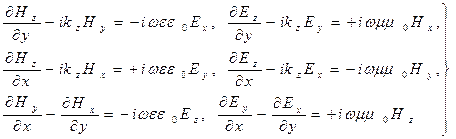(6)

Система уравнений (6) является основой для рассмотрения частных случаев распространения электромагнитной волны в прямолинейном волноводе произвольного поперечного сечения.

Интересно отметить одну существенную особенность системы уравнений (6). Ось z по условию является направлением распространения электромагнитной волны. При рассмотрении электромагнитных волн в неограниченной среде мы неоднократно убеждались, что электромагнитная волна является поперечной волной. Но если в системе уравнений (6) положить 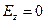и 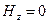, то останется система уравнений

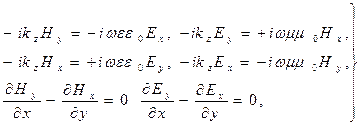
которая допускает только две возможности: или решение для амплитуд электромагнитного поля тривиально, или величина 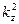является отрицательной величиной, т.е. 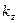является мнимой величиной, а рассматриваемые нами электромагнитные волны перестают быть бегущими волнами. Обе эти возможности не удовлетворительны с физической точки зрения. Остаётся смириться с тем, что в волноводах с поперечным сечением конечных размеров могут существовать не поперечные волны.

Система уравнений (6) может быть «разбита» на две независимые системы, в одной из них выполнено условие 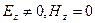, а во второй – наоборот 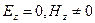. Рассмотрение частных случаев проще, чем рассмотрение явления в целом, общее решение представляет собой суперпозицию частных решений в силу линейности исходной теории.

1. Электромагнитная волна первого типа (волна Е-типа).

Рассмотрим физическую ситуацию, для которой выполнено условие 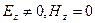. Система уравнений (6) приобретает при этом вид:

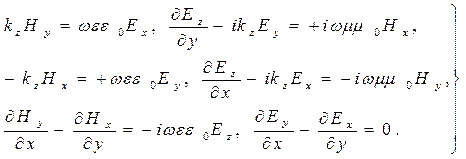(7)

Из системы уравнений (7) следует уравнение Гельмгольца для амплитуды продольной компоненты напряжённости электромагнитной волны:

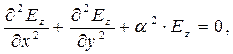
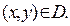(8)

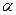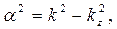
Параметр в уравнении (8) определён соотношениями 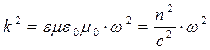(9):

. (9)

Величина n в определениях (9) является величиной показателя преломления, с – скорость распространения электромагнитной волны в вакууме (бесконечное пространство), 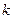- модуль волнового вектора электромагнитной волны в вакууме. Как получено уравнение (8)? Второе уравнение системы (7) надо продифференцировать по переменной у, четвёртое уравнение системы (7) надо продифференцировать по переменной х и результаты сложить с учётом возможности исключения других амплитуд с использованием остальных уравнений системы (7). При этом используется условие обращения в нуль дивергенции напряжённости электрического поля и пятое уравнение системы (7). Привлекательность полученного результата состоит в том, что мы получили уравнение для одной искомой функции и это уравнение – уравнение канонической формы.

Легко проверить, что все остальные амплитуды явным образом выражаются через функцию :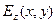

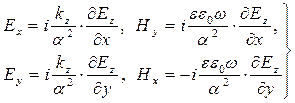(10)

Например, первое из соотношений (10) получается, если в четвёртое уравнение системы (7) подставить первое уравнение той же системы и воспользоваться определениями (9).

Все уравнения электродинамики удовлетворены, если функция 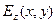удовлетворяет уравнению (8) и справедливы определения (9) и зависимости (10). Однако построение физико-математической модели нельзя считать законченным. Необходимо рассмотреть систему условий на границе раздела «диэлектрик - идеальный проводник», вытекающих из интегральной формы уравнений электродинамики.

На рис.1 показано поперечное сечение рассматриваемого волновода, ориентация составляющих вектора напряжённости электрического поля вдоль осей х и у, ось z направлена перпендикулярно плоскости рисунка и «на нас», направление единичного вектора внешней нормали 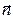к элементарному участку контура и положительное направление обхода контура – единичный вектор касательного направления 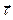. Пусть угол 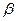является углом между направлением нормали и

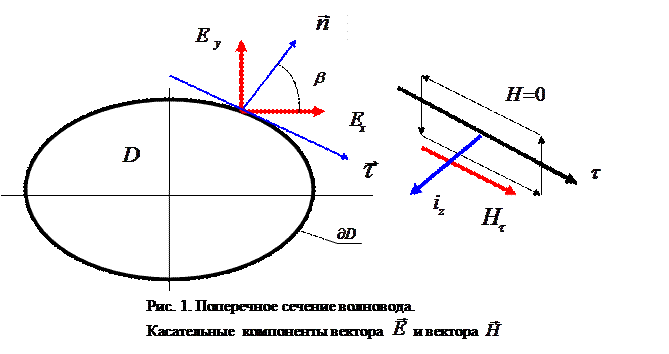
направлением оси х декартовой системы координат. На правой части рисунка показан вспомогательный контур, используемый ниже в теореме о циркуляции вектора напряжённости магнитного поля при формулировке граничных условий на боковой поверхности волновода.

Поскольку материал стенки волновода считается бесконечно проводящим, напряжённость электрического поля в стенке волновода равна нулю. Для компонент вектора напряжённости электрического поля на границе со стенкой волновода потребуем выполнения условий:

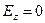на 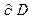. (11)

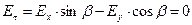
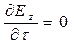. (12)

Физически необходимость условия (12) становится очевидной, если принять во внимание соотношения (10). Математически условие (12) является следствием условия (11). Необходимое условие непрерывности касательных компонент вектора напряжённости электрического поля при переходе через границу раздела двух сред выполнено.

Условие непрерывности нормальных компонент вектора магнитной индукции должно быть выполнено с учётом обращения в нуль вектора магнитной индукции в материале стенки волновода: если вектор напряжённости электрического поля в стенке волновода равен нулю, то вектор магнитной индукции тоже равен нулю: напряжённости электрического и магнитного полей в электромагнитной волне линейно связаны друг с другом и эта связь является однородной. Вычислим нормальную к контуру 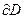компоненту напряжённости магнитного поля (напомним, что 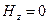всюду): 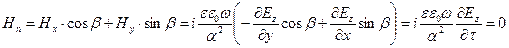. (13)

Условие непрерывности нормальных составляющих вектора магнитной индукции при переходе через границу раздела двух сред (13) автоматически выполнено как следствие условий (11) и (12).

Поскольку касательные компоненты вектора напряжённости магнитного поля в материале стенки волновода обращаются в нуль, величина 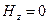, касательная компонента вектора напряжённости магнитного поля на границе области D

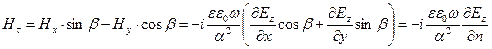(14)

определяет величину и направление поверхностной плотности тока проводимости на границе раздела:

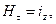
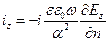. (15)

Нормальная к поверхности раздела компонента вектора 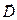вне области D равна нулю. Аналогичная величина в области D пропорциональна нормальной составляющей вектора напряжённости электрического поля:

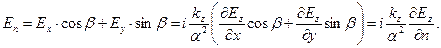(16)

Эта величина не обязательно равна нулю, поэтому на границе раздела приходится постулировать существование поверхностной плотности 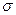сторонних электрических зарядов:

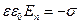
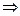
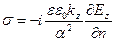. (17)

Интересно отметить прямую пропорциональную зависимость между величиной поверхностной плотности сторонних электрических зарядов (17) и величиной поверхностной плотности токов проводимости на границе раздела сред(15):

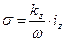. (18)

В заключение рассмотрим закон сохранения электрического заряда на поверхности раздела сред. В стенке волновода объёмная плотность токов проводимости 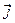обращается в нуль, поскольку отсутствует напряжённость электрического поля. Во внутренней области волновода объёмная плотность токов проводимости 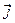обращается в нуль, поскольку среда внутри волновода является непроводящей. Таким образом, изменение величины 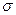в точке наблюдения с течением времени может происходить только за счёт расходимости вектора поверхностной плотности токов проводимости:

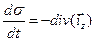. (19)

С учётом гармонического закона изменения рассматриваемых физических величин с течением времени и зависимости (15) получаем последовательность соотношений

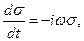
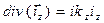
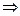
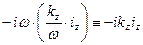, (20)

приводящей к тождеству. Закон сохранения электрического заряда на поверхности раздела сред выполнен.

Таким образом, приходим к выводу, что описанная математическая модель явления не противоречит физическим законам классической электродинамики.