Метод конечных элементов (МКЭ).

Метод конечных элементов в современном моделировании физических процессов, особенно в механике сплошных сред и электродинамике, занимает одно из важных мест. В мире разрабатывается множество программ, специальных и общего назначения, использующих методы конечных элементов. Ниже основные идеи МКЭ продемонстрированы на примере решения одномерного неоднородного уравнения второго порядка с граничными условиями первого рода.

Рассмотрим следующую краевую задачу:

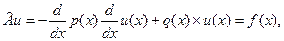
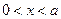(1)

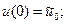
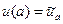. (2)

Введём следующее определение скалярного произведения двух функций:

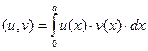. (3)

Если выполнено условие (u,v)=0, говорят, что функции u(x) и v(x) ортогональны на интервале (0,а). В вариационном исчислении доказано, что исходная краевая задача (1)-(2) эквивалентна задаче минимизации функционала

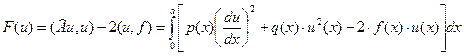. (4)

Ниже для упрощения выкладок зависимости p(x) и q(x) будем считать постоянными величинами. Отрезок [0,a] разбиваем на N, для простоты одинаковых, интервалов с шагом h=a/N. Пронумеруем концы интервалов («узлы» конечных линейных элементов системы) 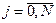. В узлах считаем, что искомая функция принимает определенные, пока неизвестные значения

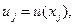
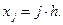(5)

Заметим, что значения 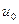и 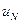по граничным условиям (2) являются заданными величинами.

Допустим, что на каждом малом интервале изменения независимой переменной x (в пределах каждого конечного элемента системы) искомая функция является линейной функцией координаты:

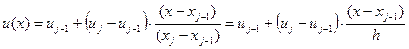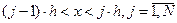, . (6)

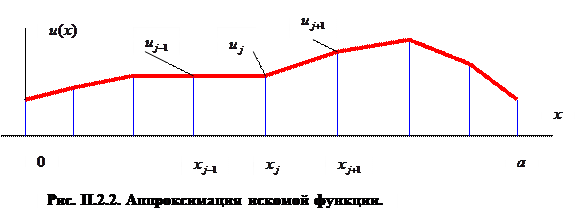зависимость (6) определяет непрерывную функцию с разрывной первой производной (рис. П.2.2):

Для произвольного конечного элемента с номером j вычислим интегралы, входящие в выражение для функционала (4):

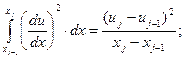(7)

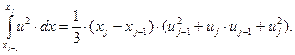(8)

Если функция f(x) аппроксимирована на рассматриваемом конечном элементе линейной функцией

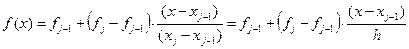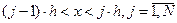, , (9)

то получим:

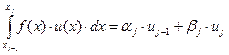, (10)

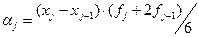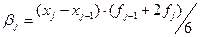, . (11)

Полученные соотношения позволяют записать конечно-элементную аппроксимацию вариационного функционала (4):

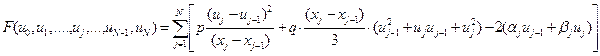. (12)

Необходимые условия экстремума функционала (12) состоят в следующем:

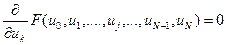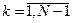, . (13)

Напомним, что необходимо иметь в виду, что имеют место граничные условия (2).

Явное выражение условий (13) с учетом равномерного разбиения области изменения независимой переменной на конечные элементы (5) имеет вид:

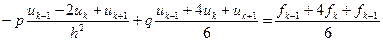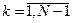, , (14)

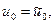
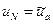. (15)

В уравнениях (14) легко просматривается разностная аппроксимация второй производной от искомой функции (множитель при величине «р») , аппроксимация искомой функции (множитель при величине «q») и аппроксимация правой части уравнения (1):

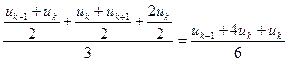. (16)

Заметим, что, как правило, прием «усреднения» искомой сеточной функции (16) повышает устойчивость вычислительного алгоритма.

В итоге мы получили, оказывается, конечно-разностную аппроксимацию исходной краевой задачи (1)-(2).

Формально систему уравнений (14)-(15) можно записать в форме векторно-матричного уравнения

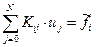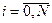, (17)

и получить решение задачи:

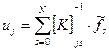. (18)

При практической реализации метода следует быть внимательным при формировании первой и последней строки матрицы 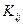и при формировании вектора-столбца .

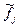В практике использования МКЭ итоговая матрица 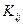, как правило, формируется наложением друг на друга матриц 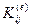, получаемых отдельно от вклада каждого конечного элемента системы с номером «е», что существенно облегчает выкладки.

Заметим, что современное математическое обеспечение компьютеров (системы MatLab, Cosmos, ANSYS и им подобные StarCD, Flow3d) содержит модули графических редакторов для задания области изменения независимых переменных для одно-, двух и (или) трехмерных задач, автоматического разбиения области на конечные элементы, тип и свойства которых можно выбрать из библиотеки конечных элементов, модули формирования уравнений и граничных условий, решатели линейных систем высокого порядка с разреженными матрицами и модули графического представления решения. Всё это значительно облегчает труд ученого-исследователя и разработчика конкретных вариантов машин, приборов и различных технических устройств.