Метод конечных разностей.

Идея метода конечных разностей состоит в замене дифференциального уравнения в частных производных конечно-разностными отношениями, для внутренних точек области, в которой это уравнение определено. Получающаяся при этом система алгебраических уравнений является неполной (незамкнутой): для граничных точек области несправедливы разностные отношения, которые справедливы для внутренних точек области. Для граничных точек области пишут разностные соотношения, которые аппроксимируют заданные граничные условия задачи. Полученную замкнутую систему алгебраических уравнений относительно «сеточной» функции, т.е. функции, определенной в узлах специально построенной сетки, решают одним из методов линейной алгебры.

Заметим, что математики в борьбе за снижение затрат машинного времени при обеспечении заданной точности вычислений разработали много различных вариантов метода конечных разностей. Ознакомиться с ними можно по руководствам А.А.Самарского, Н.Н.Яненко, С.К.Годунова, Р.Рихтмайера и К.Мортона, П.Поттера и др.

Заметим также, что математические пакеты современного специального математического обеспечения персональных компьютеров (MatLab, например) содержат «решатели» двумерных, а в более специализированных пакетах – и трехмерных линейных и нелинейных задач математической физики, среди которых краевые задачи для уравнений Лапласа или Пуассона – это одни из самых простых задач.

Для иллюстрации метода снова рассмотри задачу Дирихле для уравнения Пуассона в двумерной прямоугольной области D={(x, y): 0<x<a, 0<y<b}:

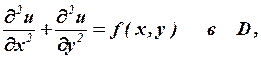
		(1)
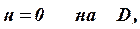
		(2)

где u(x, y) – искомая функция, f(x, y) – известная функция, 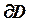- граница области D.

В области D построим «сетку»: отрезок оси х [0, a] разобьем на N_a интервалов с шагом h_a :

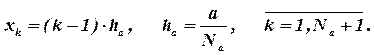
(3)

отрезок оси у [0, b] разобьем на N_b интервалов с шагом h_b

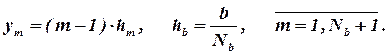
(4)

Узлом разностной сетки является пересечение прямых x=x_k и y=y_m, т.е. точка (x_k, y_m).

Введем в рассмотрение сеточную функцию:

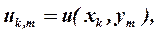
(5)

сеточная функция определена только в узлах разностной сетки. Если бы величины 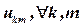,были определены (т.е. если было бы построено решение разностной задачи), значения 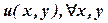можно было бы рассчитать с помощью интерполяции.

Если частную производную по координате х аппроксимировать разностным отношением вида

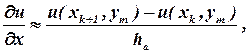
(6)

то вторую производную по координате х можно записать в форме:

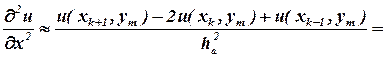
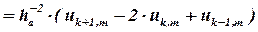
(7)

Аналогичное соотношение напишем и для частной производной по координате у:

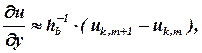
(8)

и для второй частной производной по координате у:

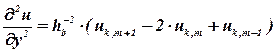
(9)

Для известной функции в уравнении (1) также введем сеточную функцию:

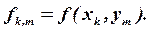
(10)

С использованием зависимостей (7), (9) и (10) из уравнения (1) получаем:

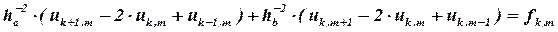
(11)

Совокупность точек разностной схемы, используемых в уравнении (11) для произвольно выбранного узла (x_k, y_m), называют шаблоном разностной схемы. На рис. П.2.1 показан шаблон описанной выше схемы: схема «крест».

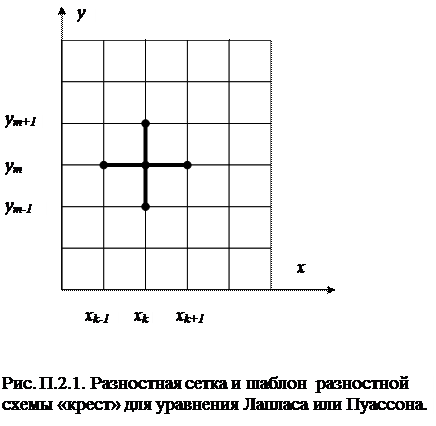
Уравнение (11) получено для случая равномерной разбивки области D узлами сетки. Возможно и неравномерное разбиение области с целью более точного учета геометрии области или физических свойств ее в отдельных подобластях. Естественно, что уравнение (11) при этом будет усложнено, хотя его основные свойства изменяются мало.

Перепишем уравнение (11) в форме:

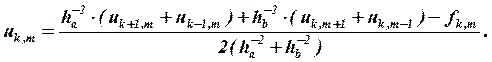
(12)

Легко видеть, что значение сеточной функции в центральной точке «креста» зависит от периферийных значений сеточной функции. Это особенно наглядно для случая f=0 и h_a = h_b:

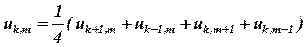
(13)

Соотношения (12), или в простейшем случае (13), справедливы для внутренних точек области D или для внутренних узлов разностной сетки: если пересечение «креста» поместить на границу, то придется рассматривать сеточную функцию на один шаг сетки за границей, т.е. там, где она принципиально не определена. Это означает, что система уравнений (11), а значит и (12) и (13) является незамкнутой. Требуется дополнительная информация. Для рассматриваемой исходной задачи необходимо выполнить дополнительные условия:

		(14)
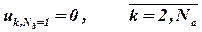
		(15)
		(16)
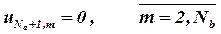
		(17)

Интересно отметить, что «угловые» точки области D не требуют своего определения: по схеме «крест» в эти точки мы никогда попадаем. Это особенно практично, когда пределы стремления точки 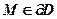к угловой точке по одной и другой линии границы не совпадают между собой.

Система уравнений (11), (14)-(17) является замкнутой и в рассматриваемом случае линейной. Если придумать алгоритм (он существует)

(18)

то описанную систему уравнений можно переписать в форме:

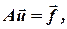
(19)

где А – соответствующая матрица коэффициентов, 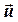- вектор-столбец искомой функции 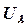, 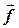- вектор-столбец известной функции 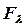, и получить решение

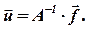
(20)

Этот метод безупречен в теоретическом отношении, но требует много машинного времени на реализацию вычислительного алгоритма.

Если сеточную задачу (11), (14) – (17) записать в форме операторного уравнения

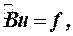
(21)

где оператор 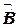определен на совокупности двухиндексных функций u_k,m, то легко видеть, что уравнение (21) можно рассматривать как результат задачи «установления» стационарного режима:

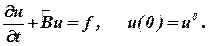
(22)

Заменим частную производную 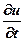разностным отношением и получим:

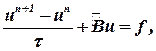
(23)

где uⁿ⁺¹ – значение u (т.е. u_k,m) на последующем временном слое, uⁿ – на предыдущем. В зависимости от того, как записать в уравнении (23) члены 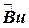, получаем либо «явную» схему

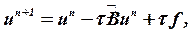
(24)

либо «неявную схему», например:

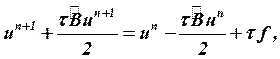
(25)

Явные схемы легче программировать, но они при некоторых значениях параметров конечно-разностной задачи могут оказаться неустойчивыми, вычисления с их использованием могут приводить к физически некорректным результатам. Схемы (24), как правило, требует использования относительно малого шага в итерационном процессе.

Необходимость рассматривать неявные схемы вызвана, зачастую, их лучшими показателями по устойчивости вычислительной процедуры. Реализация расчетов по многомерным неявным схемам основана на «методе переменных направлений» с применением «метода прогонки».

Вопросы точности аппроксимации исходной задачи конечно-разностной задачей, сходимости решения конечно-разностной задачи к точному решению исходной задачи, устойчивости вычислительного алгоритма – это вопросы соответствующего раздела вычислительной математики.