Метод разделения переменных (метод Фурье).

Метод разделения переменных известен около двухсот лет. Его возможности продемонстрируем при нахождении решения задачи Дирихле для уравнения Пуассона в двумерной прямоугольной области D={(x, y): 0<x<a, 0<y<b}

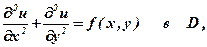
		(1)
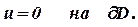
		(2)

Здесь u(x, y) – искомая функция, f(x, y) – известная функция, через 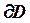обозначена граница области D. Заметим, что задачи с неоднородными граничными условиями с помощью подходящей замены искомой функции часто можно свести к рассматриваемой задаче (1) - (2).

В качестве подготовительного шага к решению исходной задачи рассмотрим вспомогательную задачу:

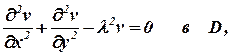
		(3)
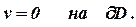
		(4)

здесь 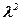- постоянная величина.

Задача (3) - (4) имеет название «спектральная задача», объяснение смысла этого термина приведено ниже. Функция v, удовлетворяющая уравнению (3) с граничными условиями (4) называется собственной функцией оператора Лапласа, а 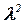- собственным значением оператора. Допустим, что функция v(x, y) представима в форме произведения двух функций, каждая из которых зависит только от одной из переменных:

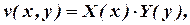
(5)

Подставим выражение (5) в уравнение (3) и результат почленно разделим на v(x,y):

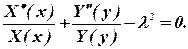
(6)

Поскольку переменные x и y независимы друг от друга, выполнение соотношения (6) возможно только, если

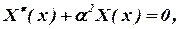
		(7)
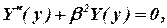
		(8)

и

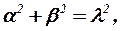
(9)

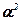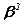где и - постоянные величины.

Общее решение уравнения (7) имеет вид:

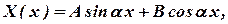
(10)

а уравнения (8)

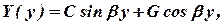
(11)

где A, B, C и G – постоянные интегрирования, они подлежат определению из граничных условий (4).

Вспомогательная функция 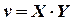обращается в ноль при х=0 (значение «у» при этом лежит в пределах 0<y<b) и при у=0 (значение «х» при этом лежит в пределах 0<x<a). В силу этих условий необходимо положить

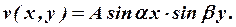
(12)

Условие обращения функции v(x, y) в ноль при х = а приводит к условию:

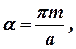
(13)

а такое же условие при y = b приводит к зависимости

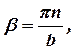
(14)

где m и n - целые положительные числа. Для того чтобы подчеркнуть зависимость функции v(x, y) от значений параметров m и n будем писать ее в форме:

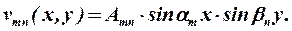
(15)

При этом

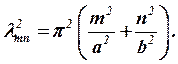
(16)

Зависимость (16) задает совокупность собственных значений оператора Лапласа, определенного на классе функций, удовлетворяющих условию (4). Эта совокупность называется «спектром» оператора.

Система собственных функций v_mn обладает свойством

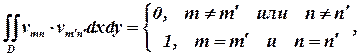
(17)

если потребовать

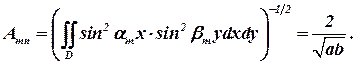
(18)

Свойство (17) – ортонормированности системы функций v_mn - позволяет представить произвольную функцию f(x, y) в форме разложения в ряд по системе собственных функций v_mn:

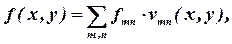
(19)

где

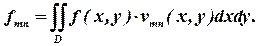
(20)

Теперь можно приступить к решению основной задачи. Пусть

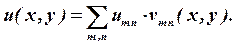
(21)

Подставим выражение (21) в уравнение (1), с учетом соотношения (19)

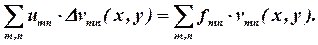
(22)

Замечая, что в силу уравнения (3) имеет место:

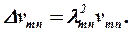
Перепишем уравнение (22) в форме:

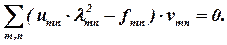
(23)

В силу линейной независимости системы собственных функций v_mn необходимо потребовать обращения в ноль выражения в круглых скобках (23) для каждого из возможных значений m и n. Это позволяет записать зависимость

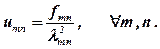
(24)

После этого зависимость (21) определена, решение задачи построено.

Заметим, что в практических расчетах ряд (21) обрывается на конечном числе членов. В математических руководствах рассмотрены условия, при выполнении которых это можно сделать.