Свойства динамических систем
Одним из важнейших свойств реальных динамических систем, как непрерывных, так и дискретных, является принцип причинности, который состоит в следующем. Реакция системы на некоторое воздействие не может начаться раньше самого воздействия. Этот принцип, вполне очевидно, выполняется в реально существующих системах, но не всегда соблюдается в математическихмоделях систем. Причем те математические модели, в которых принцип причинности нарушается, не всегда являются бесполезными: они могут пригодиться для исследования, расчетов и т.п. Однако как только возникает вопрос о практической реализации подобной модели, то выясняется, что в точности это невозможно, хотя можно реализовать различные приближенные модели (в которых принцип соблюдается). В связи с этим одна из проблем теории динамических систем заключается в выяснении условий физической реализуемости теоретических моделей, которые представляют собой конкретные ограничения, накладываемые на модель при соблюдении принципа причинности.
Рассмотрим условие физической реализуемости на примере непрерывной линейной модели.
Пример. Математическая модель идеального дифференцирующего звена описывается передаточной функцией (ПФ):
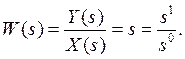
Из теории автоматического регулирования (ТАР) известно, что условие физической реализуемости для линейных моделей динамических систем, которые представляют собой дробно-рациональные функции комплексной переменной s, заключается в том, что порядок полинома по степеням s в числителе ПФ не должен превышать порядка полинома в знаменателе ПФ. То есть, если в общем случае
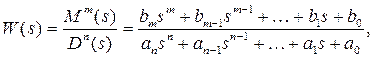
то условие физической реализуемости выражается неравенством: 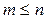 .
.
В нашем примере это условие нарушено, т.к. m = 1, а n = 0. Действительно, легко убедиться, что невозможно физически реализовать идеальное дифференцирующее звено с передаточной функцией W(s )= s, если рассмотреть, что должно получиться на выходе такой модели, когда на его вход подается традиционное единичное ступенчатое воздействие.
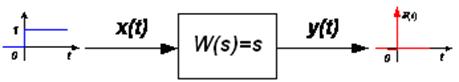
Рис. 2.7. Модельидеального дифференцирующего звена
Как показано на рис. 2.7, на выходе должна получиться так называемая d-функция Дирака, представляющая собой мгновенный по времени и бесконечный по величине импульс, потому что производная от ступенчатой входной функции в точке t = 0 терпит разрыв (стремится к ∞). Очевидно, что такой импульс практически реализовать невозможно. Поэтому для практических целей используют реальное дифференцирующее звено, которое описывается ПФ вида: 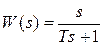 . Здесь m=1 и n=1, т.е. условие физической реализуемости
. Здесь m=1 и n=1, т.е. условие физической реализуемости 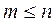 уже выполняется. На выходе такого звена получается переходная функция в виде затухающей экспоненты (рис. 2.8).
уже выполняется. На выходе такого звена получается переходная функция в виде затухающей экспоненты (рис. 2.8).
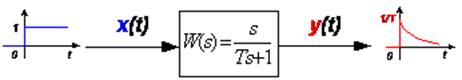
Рис. 2.8. Модельреального дифференцирующего звена
Причем этот выходной импульс получается тем более узким и более высоким, т.е. тем более близким к d-функции, чем меньше постоянная времени T. Соответственно тем точнее звено выполняет операцию дифференцирования. При увеличении T, наоборот, задний фронт выходного импульса затягивается, экспонента более медленно стремится к нулю, а максимальное значение импульса становится все меньше (рис. 2.9).
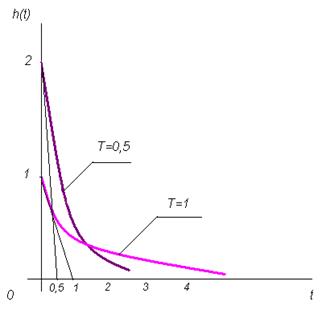
Рис. 2.9. Переходные функции реального дифференцирующего звена для разных значений постоянной времени Т
Следовательно, переходная функция все меньше напоминает d-функцию, и операция дифференцирования таким звеном выполняется все менее точно.
Вопросы к разделу 2.3
- В чем заключается принцип причинности реальных систем?
- В чем состоит условие физической реализуемости для линейных моделей динамических систем?
Дата добавления: 2021-09-07; просмотров: 537;











