Определить вид движения, начальную скорость и касательное ускорение точки
Пример 1. По заданному закону движения S =10 + 20t — 5t2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)
 Решение
Решение
1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at = — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S' = 20 - 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).
 Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?
Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?
Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v2/r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.

Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).
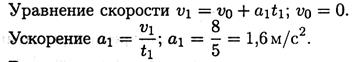
Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
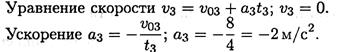
2. Путь, пройденный за время движения, будет равен:
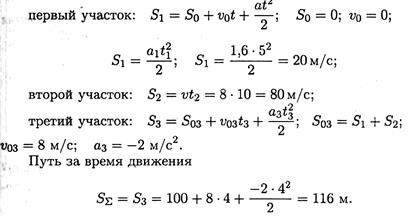
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
v = vо + at = 0.
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = - v0/t
2. Записываем уравнение пути: S = vot/2 + at2/2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):

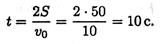
Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с2. Значит, движение точки равнопеременное (a = at = —10 м/c2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения

3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с2-мм) (1 м/с2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.
 Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.
Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.
Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:
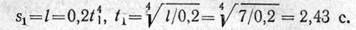
Уравнение изменения скорости
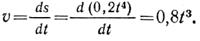
Скорость точки в положении 1
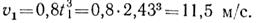
Уравнение изменения касательного ускорения
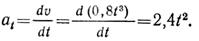
Касательное ускорение точки в положении 1
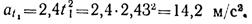
Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с2.
Нормальное ускорение точки в начале криволинейного участка
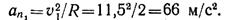
Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:
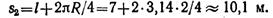
Время, необходимое для перемещения точки из положения 0 в положение2,
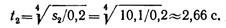
Скорость точки в положении 2
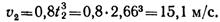
Касательное ускорение точки в положении 2
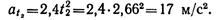
Нормальное ускорение точки в положении 2
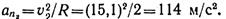
Ускорение точки в положении 2
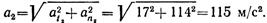
Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).
 Пример 7. Точка движется по заданной траектории (рис. 1.45, а) согласно уравнению s = 5t3(s — в метрах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t1, когда скорость точки v1 = 135 м/с.
Пример 7. Точка движется по заданной траектории (рис. 1.45, а) согласно уравнению s = 5t3(s — в метрах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t1, когда скорость точки v1 = 135 м/с.
Решение
Уравнение изменения скорости
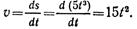
Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:
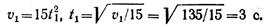
Определим положение точки на траектории в момент 3 с:
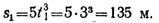
Дуга окружности длиной 135 м соответствует центральному углу
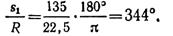
Уравнение изменения касательного ускорения
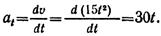
Касательное ускорение точки в момент tt
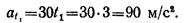
Нормальное ускорение точки в момент tt
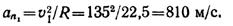
Ускорение точки в момент tx
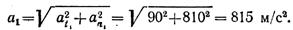
Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б
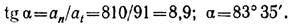
Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела
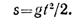
Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:
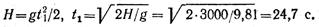
Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука
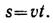
Время достижения звуком поверхности земли
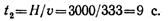
Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли
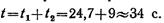
Пример 9. По заданным уравнениям движения точки x = 2t2, y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:
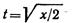
и подставим это значение во второе уравнение:
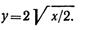
Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям
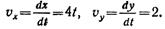
Находим скорость точки
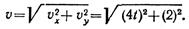
При t = 2 с получаем
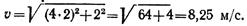
Находим составляющие ускорения точки
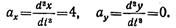
Ускорение точки
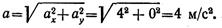
Дата добавления: 2017-09-01; просмотров: 12877;











