К. п. д. процесса движения ГЖС

На каждой кривой q(V) имеется еще одна характерная и очень важная точка, точка так называемой оптимальной производительности, соответствующая наибольшему к. п. д. Если проанализировать произвольную кривую q(V), для которой e = const, то для нее будут справедливы следующие рассуждения.

Из определения понятия к. п. д. следует, что

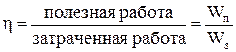. (7.2)

Полезная работа заключается в поднятии жидкости с расходом q на высоту L - h, так что

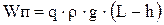. (7.3)

Затраченная работа - это работа газа, расход которого, приведенный к стандартным условиям, равен V. Полагая для простоты, что процесс расширения газа изотермический, на основании законов термодинамики идеальных газов можем записать

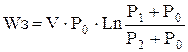, (7.4)

где Р₁ + Рo - абсолютное давление у башмака; Р2 + Ро - то же на устье, Ро - атмосферное давление.

Подставляя (7.3) и (7.4) в (7.2), получим

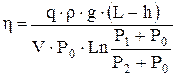. (7.5)

В (7.5) все величины, кроме q и V, постоянны, так как рассматривается одна кривая q(V), для которой ε = const. Следовательно, для данной кривой

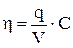, (7.6)

где С - константа.

Поэтому к. п. д. будет иметь максимальное значение в той точке, в которой отношение q / V максимально. Но q / V = tg φ, так как q - ордината, V - абсцисса, φ - угол наклона прямой, проведенной из начала координат через данную точку (q, V). Только для касательной tgφ будет иметь максимальное значение, так как только для нее угол φ максимален. Поэтому в точке касания прямой, проведенной из начала координат с кривой q(V), получаются такой дебит q и такой расход газа V, при которых к. п. д. процесса будет наибольшим. Расход q при максимальном к. п. д. называют оптимальным дебитом qoпт.

Таким образом, для любой кривой q(V), имеющей ε = const, оптимальный расход жидкости определится как точка касания касательной, проведенной из начала координат.