Плотность газожидкостной смеси

Через данное сечение трубы при движении по ней ГЖС проходит некоторое количество газа и жидкости. Можно представить, что все газовые пузырьки занимают в сечении трубы суммарную площадь fг, а жидкость - остающуюся площадь в том же сечении fж, так что

,

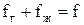где f - площадь сечения трубы (рис. 7.8). Плотность ГЖС в таком случае определится как средневзвешенная

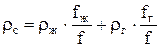, (7.18)

где ρж и ρг - плотность жидкости и газа при термодинамических условиях сечения.

Обычно fг / f обозначают через φ. Тогда fж / f = 1 - φ,

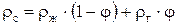. (7.19)

Величина φ = fг / f называется истинным газосодержанием потока.

Обозначим V - объемный расход газа через данное сечение; q - объемный расход жидкости через то же сечение; Сг - линейная скорость движения газа относительно стенки трубы; Сж - линейная скорость движения жидкости относительно стенки трубы.

Тогда можно записать следующие соотношения:

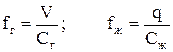. (7.20)

и

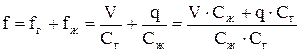. (7.21)

Подставляя (7.20) и (7.21) в (7.18) и делая некоторые сокращения, получим

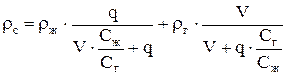, (7.22)

В восходящем потоке газ движется быстрее жидкости, так как на него действует архимедова сила выталкивания. Обозначим

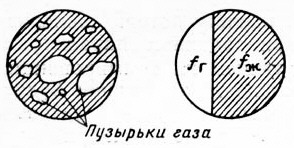
Рис. 7.8. Среднестатистические площади в трубе, занятые газом и жидкостью

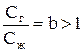, (7.23)

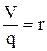. (7.24)

Разделив числитель и знаменатель в (7.22) на q и вводя новые обозначения согласно (7.23) и (7.24), получим

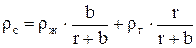, (7.25)

где r - газовый фактор, приведенный к термодинамическим условиям рассматриваемого сечения.

При Сг = Сж b = 1 и из (7.25) следует

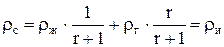. (7.26)

Этот случай соответствует идеальным условиям, при которых образуется идеальная смесь плотностью ρи. Относительная скорость газа (по отношению к жидкости)

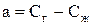, (7.27)

или

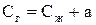. (7.28)

Подставляя (7.28) в (7.23), получим

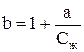, (7.29)

Поскольку а > 0, то b > 1. Увеличение скорости газа при неизменном объемном расходе V уменьшает fг, следовательно, увеличивает fж. В результате плотность смеси, как это следует из (7.18) и (7.19), увеличивается. Таким образом, явление скольжения газа (a > 0) при неизменных объемных расходах q и V приводит к утяжелению смеси по сравнению с идеальным случаем. Поэтому чем больше а, тем больше потребуется давление на забое для поднятия данного количества жидкости.

Плотность реальной смеси

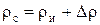, (7.30)

где Δρ - увеличение плотности смеси, обусловленное скольжением. Для определения Δρ к (7.25) прибавим и отнимем ρи согласно (7.26), получим

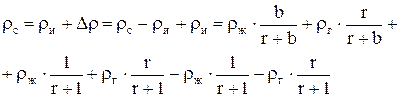
Группируя слагаемые и делая некоторые преобразования, имеем

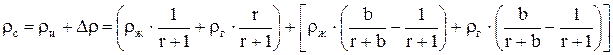
или после приведения к общему знаменателю в квадратных скобках и группировки слагаемых найдем

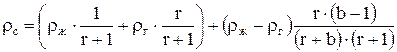. (7.31)

Из сопоставления (7.31), (7.30) и (7.26) следует

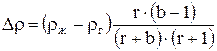. (7.32)

При b = 1 (отсутствие скольжения газа Сг = Сж) числитель в (7.32) обращается в нуль и Δρ = 0. Утяжеление ГЖС не происходит. С увеличением b (b > 1) Δρ монотонно увеличивается (рис. 7.9). Заштрихованная часть графика показывает увеличение плотности ГЖС за счет скольжения газа.

Из формулы (7.29) видно, что при одной и той же относительной скорости газа (a = const) b уменьшается при увеличении Сж, т. е. расхода жидкости. Отсюда следует важный для практики вывод - переход на трубы малого диаметра при определенных условиях за счет увеличения Сж уменьшит величину b, а это в свою очередь повлечет уменьшение Δρ.

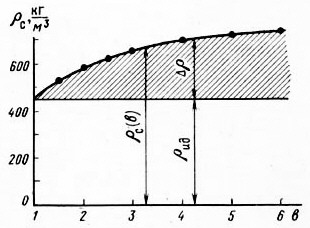
Pиc. 7.9. Изменение плотности ГЖС в результате скольжения газа

Поэтому подъем ГЖС может быть осуществлен при меньшем давлении в нижней части трубы (при меньшем забойном давлении). Однако целесообразность перехода на трубы меньшего диаметра должна быть проверена расчетом, так как при этом возрастут потери давления на трение.

В теории движения ГЖС существуют важные понятия, через которые определяется плотность смеси. Это расходное газосодержание β и истинное газосодержание φ. Расходное газосодержание потока ГЖС определяется как отношение объемного расхода газа V к общему расходу смеси V+q:

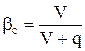. (7.33)

Истинное газосодержание потока ГЖС учитывает скольжение газа и поэтому является отношением площади, занятой газом fг, ко всему сечению трубы f:

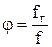. (7.34)

Тогда

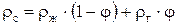. (7.35)

Из сопоставления (7.35) и (7.25) следует

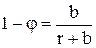. (7.36)

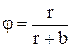. (7.37)

Разделив в (7.33) числитель и знаменатель на q и используя обозначение (7.24), получим

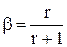. (7.38)

Отнимая в (7.38) по единице и меняя знак, получим

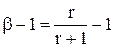. (7.39)

или

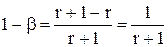. (7.39)

Сопоставляя (7.39), (7.38) и (7.26), видим, что

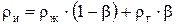. (7.40)

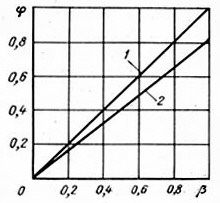
Рис. 7. 10. Зависимость φ от β при отсутствии скольжения газа

(β = φ, линия 1) и при скольжении ( φ < β, линия 2)

Таким образом, плотность идеальной смеси (7.40) определяется расходным газосодержанием β, а плотность реальной смеси (7.35) - истинным φ.

Найдем формулы связи между φ, β, b и r. Из (7.37) и (7.38) имеем

,

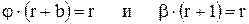откуда

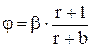. (7.41)

Решая (7.38) относительно г, найдем

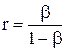. (7.42)

Подставляя (7.42) в (7.41), получим

.

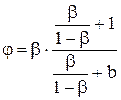Откуда после преобразований

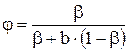. (7.43)

Решая (7.43) относительно b, получим

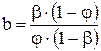. (7.44)

При движении ГЖС возможны два предельных случая, когда по трубе движется одна жидкость fг = 0, следовательно, φ также равно нулю, и когда по трубе движется один газ fж = 0. Аналогично и для расходного газосодержания β. Поэтому физически возможными пределами изменениями φ и β будут 0 < φ <1, 0< β < 1. При отсутствии скольжения газа относительная его скорость равна нулю (а = 0), следовательно, Сг = Сж, b = 1 и из формулы (7.43) φ = β.

Таким образом, φ(β) для идеального подъемника будет являться прямой в виде диагонали квадрата линия 1 (рис.7.10).

Во всех других случаях при b > 1 , т. е. при а > 0 (Сг > Сж), получим φ = β .

На диаграмме φ(β) линия 2 проходит ниже диагонали. Чем больше скольжение, т. е. чем больше а, а следовательно, и b, тем ниже пройдет линия φ(β).

Относительная скорость газа а зависит от следующих факторов: дисперсности газовых пузырьков, а следовательно, структуры движения ГЖС; вязкости жидкой фазы; разности плотностей газа и жидкости, от которой зависит подъемная сила; диаметра трубы и газонасыщенности потока ГЖС.

Попытки теоретического определения величины а не дают надежных результатов. Поэтому оценка относительной скорости газа проводится главным образом экспериментально и составляет основной предмет исследований. По некоторым рекомендациям предлагается принять φ = 0,833·β во всем диапазоне значений β представляющем практический интерес. Величина β всегда известна, так как расходами V и q либо задаются, либо вычисляют для заданных термодинамических условий.

Формулы перехода

В литературе по вопросам движения ГЖС для вычисления рс различные авторы используют различные выражения и различные подходы к определению этой важной величины. Покажем, что все возможное разнообразие подходов к определению ρс может быть осуществлено с помощью формул перехода, связывающих основные величины, определяющие ρс, такие как β, φ, r, b, а, C, Cж, Сг.

Ранее были получены следующие выражения:

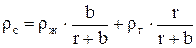, (7.45)

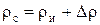, (7.46)

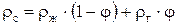. (7.47)

где

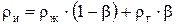. (7.48)

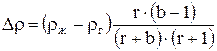. (7.49)

Из сопоставления (7.45) и (7.47) следует

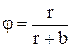. (7.50)

Так как при отсутствии скольжения Сг = Сж, b = 1. Из сопоставления (7.45) и (7.48) получим

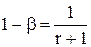. (7.51)

Используя (7.50) и (7.51) и подставляя их в (7.49), получим

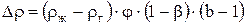. (7.52)

Решая (7.50) относительно r, найдем

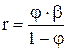. (7.53)

Решая (7.51) относительно r, найдем

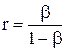. (7.54)

Приравнивая (7.53) и (7.54) и решая относительно b, найдем

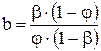. (7.55)

Решая (7.55) относительно φ, найдем

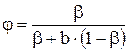. (7.56)

При необходимости вычислить φ через относительную скорость газа а такое вычисление может быть сделано следующим образом. Имеем

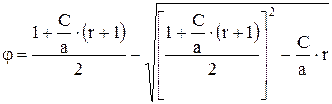. (7.57)

Формулу (7.57) можно выразить через β

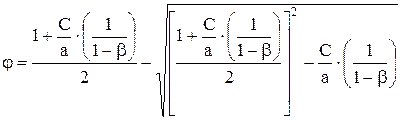. (7.58)

При определении ρс через величину b необходимо знать действительную скорость жидкости Сж и относительную скорость газа а. Можно легко вывести формулу для Сж

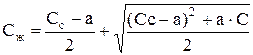. (7.59)

Здесь С - приведенная скорость жидкости , равная q / f.

Увеличение плотности смеси Δρ можно выразить через φ и β следующим образом:

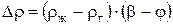. (7.60)

Таким образом, используя формулы перехода, всегда можно перейти от одних величин, определяющих истинную плотность смеси, таких как φ или b, к другим величинам, таким как а, Сж и пр.