Напряжённость магнитного поля.

Циркуляция вектора магнитной индукции 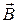по замкнутому контуру в магнитной среде, очевидно, должна рассчитываться с учетом всех токов, которые чисто условно разделены на ток проводимости 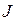и ток намагничения :

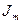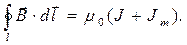(1)

Анализируя совокупность соотношения (3) предыдущего раздела и соотношения (1), замечаем, что имеет место зависимость

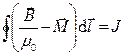. (2)

Полученная зависимость удобна тем, что в ее правой части стоит величина тока проводимости J, не связанная с молекулярной структурой вещества.

Введем в рассмотрение вектор напряженности магнитного поля :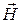

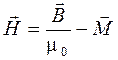
(3)

и получим интегральное соотношение

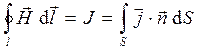, (4)

и соответствующее ему (следствие классической теоремы Стокса) дифференциальное соотношение

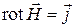, (5)

где 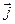- объёмная плотность тока проводимости. Физическая размерность вектора напряжённости магнитного поля совпадает с размерностью вектора намагничения среды 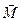и равна 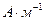. В качестве единицы измерения вектора напряжённости магнитного поля используют эту же величину 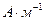. В магнитостатике для некоторых геометрических конфигураций электрических токов проводимости с высокой степенью симметрии интегральное соотношение (4) позволяет рассчитывать поле магнитной напряжённости .

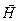7.4.5. Магнитные свойства среды.

При феноменологическом подходе к описанию магнитной среды, не затрагивающем молекулярно-кинетическое строение среды, полагают, что

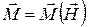, (1)

причем для многих веществ и “слабых” магнитных полей эта зависимость линейная и однородная:

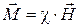, (2)

где 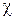- магнитная восприимчивость среды (величина безразмерная). При феноменологическом описании среды зависимость (2) и, в частности, величина 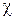считаются известными или из опыта, или из рассмотрения соответствующих молекулярно-кинетических моделей среды. Зависимость (2) позволяет записать “материальное уравнение” магнитной среды в форме

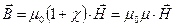, (3)

где

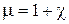(4)

носит название “магнитная проницаемость” среды (величина безразмерная).

Вопрос о плотности некомпенсированных молекулярных токов решается прямым вычислением:

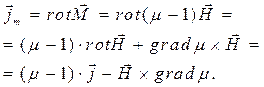(5)

Легко видеть, что плотность токов намагничения 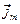обусловлена токами проводимости и неоднородностью магнитных свойств среды.

Варианты построения теории магнитного поля в веществе.

Справедливость результатов настоящего раздела, строго говоря, существенно зависит от принятой формы записи магнитных дипольных моментов элементарных токов (1) раздела 7.4.3. В более полных руководствах по классической электродинамике приняты две схемы введения векторного поля намагниченности среды. Согласно первой схеме в качестве постулата принимают уравнение (4) того же раздела и методами векторного анализа доказывают, что из общего определения магнитного момента системы токов

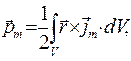
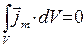(1)

следует соотношение

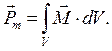(2)

Выражение (2) определяет физический смысл вектора намагниченности 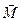как магнитный момент 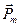объёма среды, занятого токами намагничения, в пересчете на единицу объёма.

Согласно второй схеме рассматривают выражение для векторного потенциала магнитного поля

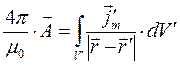(3)

в точках пространства, достаточно удаленных от рассматриваемого объёма среды с токами намагничения,

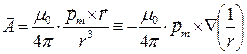(4)

и переходят от дифференциальных операций по координатам точки наблюдения к дифференциальным операциям по координатам точек расположения элементарных объёмов среды с токами намагничения. После достаточно сложных выкладок приходят к результату:

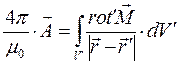. (5)

Сравнивая между собой выражения (3) и (5), приходят к заключению, что справедливо уравнение (4) раздела 7.4.3

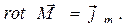
Таким образом, основные макроскопические представления о векторном поле намагничения среды можно считать обоснованными.

Заметим, что вектор намагниченности среды 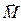как локальная физическая характеристика среды не зависит от выбора начала координат. В основе её определения лежит понятие магнитного момента системы токов. Если определить вектор намагниченности соотношением

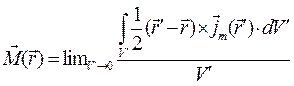, (6)

т.е. в основу определения вектора намагничения среды положить магнитный момент системы токов относительно точки наблюдения и рассматривать объём среды с токами в малой окрестности точки наблюдения, то прямым вычислением приходим к результатам:

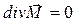(7)

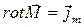. (8)

Первое из этих уравнений свидетельствует об отсутствии специфических магнитных зарядов, а второе является необходимым условием возможности введения понятия «вектор напряженности магнитного поля».

Покажем справедливость уравнений (7) и (8). Предполагая возможность дифференцирования по параметру под знаком интеграла в определении (6) и возможность поменять порядок вычисления дивергенции по координатам точки наблюдения и вычисления предела по координатам точек расположения элементов объёма среды с токами, получаем

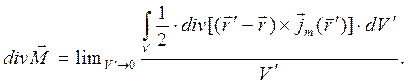(9)

Далее используем известные тождества векторного анализа (при желании или сомнении их можно проверить прямым вычислением)

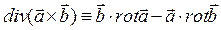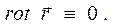, (10)

В результате получаем уравнение (7). При проверке справедливости уравнения (8) используем тот же методический приём и тождество

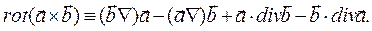(11)

Напомним, что операция rot проводится по координатам точки наблюдения. В этом случае, очевидно, имеют место соотношения

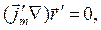
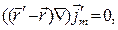
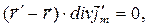
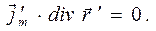
С их учётом получаем

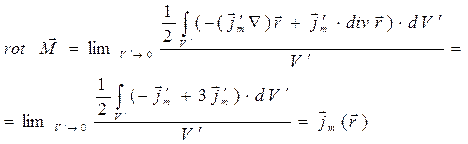(12)

На этом закончим обсуждение вопросов феноменологического описания векторного поля намагниченности среды и векторного поля напряженности магнитного поля.