Магнитное поле в веществе. Гипотеза Ампера о молекулярных токах. Намагниченность вещества. Свойство намагниченности вещества. Напряженность магнитного поля.

Все природные вещества в той или иной мере обладают магнитными свойствами, эти вещества называют магнетиками. Частными случаями магнетиков являются пара- и диамагнетики, ферромагнетики и антиферромагнетики...

В начале исследования магнетизма для объяснения свойств постоянных магнитов Ампер выдвинул смелую по тем временам гипотезу о существовании так называемых “молекулярных токов”, совокупность которых объясняет магнитные свойства вещества. В настоящее время гипотеза Ампера представляется чуть ли не очевидной, физические механизмы, ответственные за магнитные свойства веществ, изучены значительно более глубоко, чем это было возможно во времена Ампера. Магнитным свойством веществ посвящены многие специальные руководства.

7.4.1. Намагниченность среды.

Рассмотрим достаточно малый объем вещества. Допустим, что суммарный магнитный момент молекулярных токов (магнитных диполей) в этом объеме равен 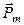. В качестве количественной характеристики магнитного состояния среды примем по определению величину намагниченности

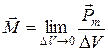. (1)

В соответствии с определением (1) намагниченность (вектор намагничения среды) 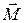представляет собой магнитный момент системы токов в физически малом объёме, рассчитанный на единицу объема среды. Намагниченность является локальной характеристикой среды, она определяется в каждой точке пространства и образует соответствующее векторное поле. Физическая размерность намагниченности равна 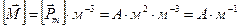(ампер на метр).

Если магнитный момент элементарного молекулярного тока равен 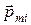, где - порядковый номер этого тока в совокупности молекулярных токов объема 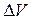, то легко получить:

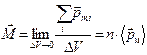, (2)

где 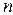- объемная концентрация элементарных молекулярных токов в рассматриваемой точке пространства, а 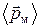- средний магнитный момент одного магнитного диполя.

7.4.2. Токи намагничения.

Совокупность элементарных молекулярных токов образует объёмную плотность 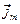и силу тока 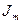намагничения. Токи проводимости с плотностью 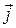и силой тока 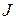связаны с носителями зарядов, которые могут относительно свободно перемещаться по проводнику. Токи намагничения могут существовать и в непроводящей электрический ток среде. Представить себе наглядно физическую связь между намагниченностью и токами намагничения можно, анализируя случай однородного распределения магнитных диполей одного направления (рис. 1). Легко видеть, что внутри выделенного элемента вещества молекулярные токи компенсируют друг друга, некомпенсированным остается только ток по поверхности выделенного объема.

Обратим внимание на то, что направление тока

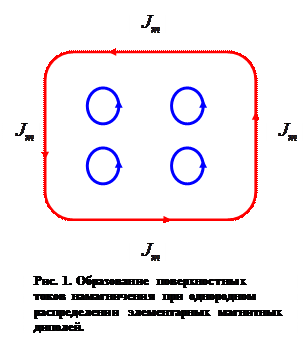
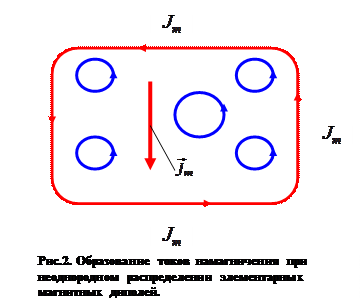
намагничения перпендикулярно ориентации магнитных диполей, то есть вектору намагничения 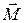. В случае неоднородного распределения магнитных диполей одного направления, например, показанного на рисунке 2, помимо поверхностных токов намагничения 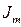возникает объёмная плотность 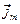токов намагничения как объёмная плотность некомпенсированных молекулярных токов.

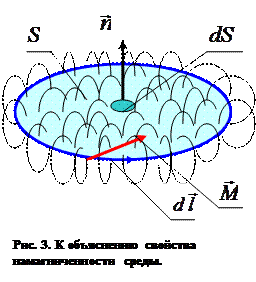
Рассмотрим поверхность 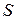в магнитном веществе, ограниченную замкнутым контуром 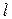с выбранным положительным направлением обхода и ориентацией нормали к элементу площади ее поверхности (рис.3). Ток намагничения определим соотношением

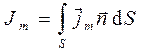, (1)

где 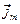возникает как плотность молекулярных некомпенсированных токов. Легко видеть, что для внутренних точек поверхности 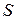молекулярные токи, каждый в отдельности, пересекают поверхность 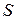в одну сторону и другую, тем самым не создавая результирующего тока намагничения. Для приграничных точек поверхности 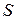имеются молекулярные токи, которые огибают контур поверхности, т. е. пересекают рассматриваемую поверхность в одном направлении, создавая тем самым некомпенсированный ток через поверхность.

7.4.3. Теорема о циркуляции намагниченности среды.

Если модуль магнитного момента отдельного магнитного диполя равен 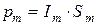, ориентация магнитного диполя относительно элемента 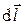описывается в среднем углом 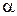, то “ометаемой” площадкой объем при перемещении на 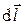составит величину 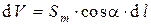. Магнитные диполи в “ометаемом” объеме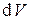 формируют ток намагничения

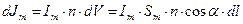, (1)

где 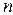- объемная концентрация магнитных диполей в окрестности элемента 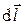контура 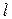. Из соотношения (1) следует

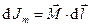. (2)

Основное свойство намагниченности 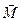проявляется в том, что имеет место интегральное соотношение

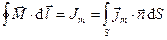, (3)

где 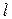- замкнутый контур, поверхность 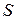натянута на этот контур, направления векторов 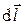и 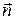согласованы между собой, и его дифференциальный аналог (следствие классической теоремы Стокса):

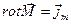. (4)

В этих соотношениях 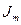- сила тока намагничения, 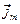- вектор объёмной плотности тока намагничения.

Заметим, что полученные соотношения являются следствием принятых в качестве исходных определений (1) и (2) раздела 7.4.1.