Двухточечные методы наведения

К двухточечным методам наведения, определяющим взаимное движение двух геометрических точек (снаряд и цель) относятся [2,3,8]:

а) метод наведения по «кривой погони»;

б) методы наведения с упреждением.

Различные двухточечные методы наведения являются частными случаями пропорционального сближения. Сущность пропорционального сближения состоит в том, что в процессе управления угловая скорость вращения вектора скорости управляемого объекта поддерживается пропорциональной угловой скорости вращения линии снаряд-цель.

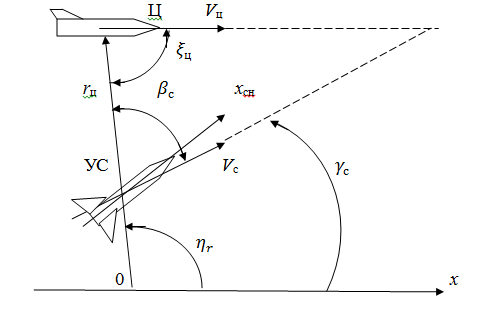
Рисунок 3.1 – Геометрические соотношения при 2-х точечных

методах наведения:

УС – управляемый снаряд, Ц – цель, х – неподвижная ось координат

Воспользовавшись обозначениями рисунка 3.1, запишем сформулированное условие пропорционального сближения

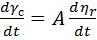, (3.4)

где А – коэффициент пропорциональности. Угол 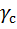определяет направление вектора скорости снаряда, а угол 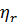- направление линии снаряд-цель. Угол 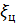между вектором скорости цели и линией снаряд-цель называют углом цели. x_сн – продольная ось снаряда.

Интегрируя уравнение (3.4), получим

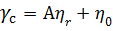. (3.5)

Заметим, что в частном случае А=1, угол - 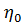будет представлять собой угол между вектором скорости снаряда и линией снаряд-цель (рисунок 3.1), т.е. угол упреждения 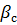. Следовательно в этом случае

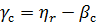. (3.6)

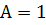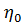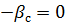I. Положим теперь в выражении (3.5) и = . Тогда получим

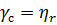. (3.7)

В этом случае система управления должна работать таким образом, чтобы вектор скорости снаряда был постоянно направлен на цель ( 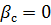). Подобное условие соответствует методу наведения по «кривой погони» (чистое преследование).

II. Если в уравнении (3.6) принять 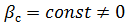, то получим метод наведения с постоянным углом упреждения. Этот метод обладает рядом недостатков, поэтому не находит широкого применения. Один из недостатков, сводится к тому, что при маневрах цели и изменениях соотношения скоростей снаряда и цели траектория полета может оказаться сильно искривленной, и перегрузки будут недопустимо велики.

III. Если в соотношении (3.4) положить

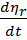=0 (3.8)

(подобное равенство получится, если в соотношении (3.4) принять 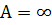), то будем иметь так называемый метод параллельного сближения, или метод последовательных упреждений.

Очевидно, что условие (3.8) выполняется в том случае, когда вектор r_ц в процессе наведения перемещается параллельно самому себе (рисунок 3.1), что и определило название метода.

IV. Можно также осуществить наведение на основе непосредственного использования уравнения (3.4) при различных конечных значениях постоянной 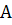(например, при 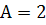). Все эти методы носят общее название «пропорциональное сближение».

Все методы в процессе наведения требуют измерения скорости вращения линии снаряд-цель, т.е. измерения значения производной 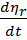. Вследствие этого принципы аппаратурного построения системы управления для всех перечисленных методов во многом идентичны.

Пространственное движение ЛА можно полностью определить, если рассматривать проекции траектории на взаимно перпендикулярные плоскости (рисунок 1.15). Поскольку кинематические уравнения в плоскостях имеют одинаковый вид, для простоты можно рассмотреть траекторию движения в одной из плоскостей. Математическое описание кинематической траектории для различных методов наведения связано с решением ряда дифференциальных и тригонометрических уравнений. При решении этих уравнений желательно получить управляющую функцию 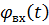или закон отклонения кинематической траектории от прямой линии, соединяющей снаряд и цель в момент пуска. Управляющая функция 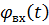может быть рассчитана или в угловых, или в линейных величинах в зависимости от метода управления снарядом.

На рисунке 3.2 показаны траектории движения ЛА по кривой погони и при параллельном сближении. Траектории построены приближенно, графическим способом, на основании равенства .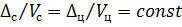

Из рисунка видно, что первая траектория сильно искривлена. Наведение

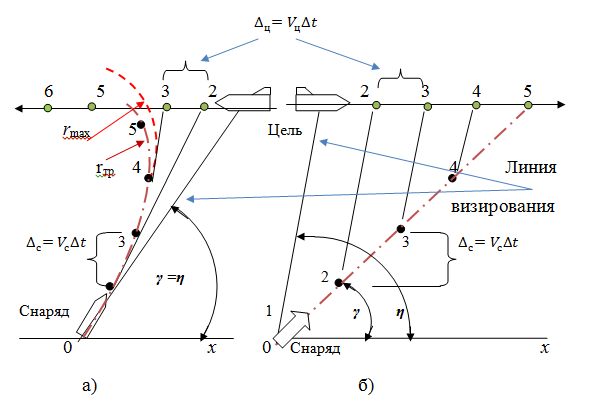
Рисунок 3.2 - Траектории движения ЛА при наведении

а) по кривой погони и б) при параллельном сближении

на быстро движущуюся цель методом кривой погони затруднительно, особенно при стрельбе навстречу, когда радиус кривизны траектории по мере приближения снаряда к цели стремится к нулю ( 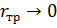). В этом случае снаряд, обладающий минимальным радиусом разворота ( 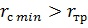), сходит с кинематической траектории. Метод наведения по кривой погони имеет практическое значение в основном только для наведения на медленно движущиеся или неподвижные цели.

В методе параллельного сближения при прямолинейном движении цели и постоянном отношении скоростей цели и снаряда угол упреждения

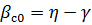постоянен и кинематическая траектория будет прямолинейной (рисунок 3.2,б), т.е. снаряд не испытывает не испытывает поперечных перегрузок. В общем случае значение угла 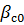будет функцией времени, так как угол ξ_ц , скорости снаряда и цели могут изменяться. Траектория снаряда при маневрах цели или при изменении скорости снаряда искривляются.

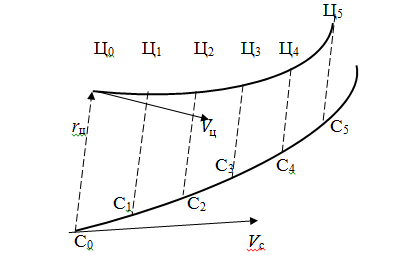
Рисунок 3.3 – Траектории при параллельном сближении

На рисунке 3.3 выдерживаются следующие очевидные равенства

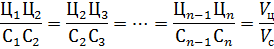
и условия параллельности линий Ц₁С₁║Ц₂С₂║…║Ц_n С_n.

Ошибка управления при методе параллельного сближения определяется как

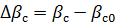, (3.9)

где 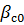- значение угла при исходном положении вектора скорости (должно подчиняться соотношению (3.10)), 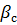- фактическое значение угла между вектором скорости снаряда 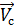и вектором 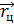. Вектор 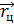перемещается параллельно самому себе. Для этого должно выполняться условие

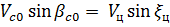. (3.10)

В первом приближении для случая 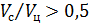считается, что при наведении на маневрирующую цель с поперечным ускорением 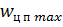, снаряд должен следовать по таким траекториям, для которых потребуется максимальное поперечное ускорение, равное 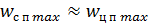. Относительно небольшие перегрузки, испытываемые снарядом, являются существенным преимуществом метода параллельного сближения.