Индуктивность коаксиального кабеля.

Коаксиальным кабелем называют систему, состоящую из прямолинейного цилиндрического проводника и охватывающей его, как правило, тонкостенной проводящей трубки кольцевого поперечного сечения. Электрический ток течет по внутреннему проводнику в заданном направлении. Точно такой же по величине электрический ток течет по внешнему проводнику в обратном направлении. Ниже рассмотрим конструкцию коаксиального кабеля, в которой внутренний проводник является тонкостенной цилиндрической оболочкой (рис. 1). Это предположение позволит нам не уточнять реальное распределение тока по внутреннему проводнику. Индуктивность коаксиального кабеля рассчитывается на единицу длины кабеля. Контур, на который натянута поверхность, пронизываемая силовыми линиями магнитного поля, охватывает плоскую радиальную поверхность между проводниками протяженностью в одну единицу длины.

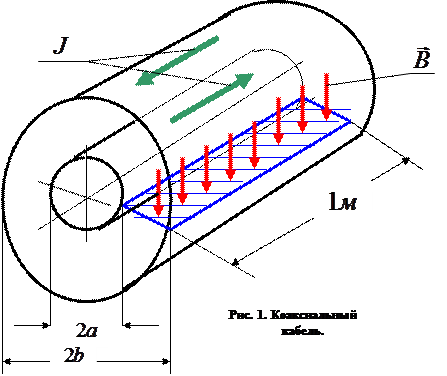
С помощью теоремы о циркуляции вектора магнитной индукции убеждаемся в том, что магнитное поле внутри первой цилиндрической оболочки 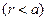и вне второй цилиндрической оболочки 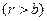равно нулю. Магнитное поле между цилиндрическими оболочками описывается выражением

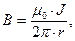
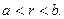(1)

Здесь и 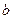- радиусы внутренней и внешней оболочек соответственно, 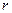- текущий радиус, 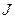- сила тока, текущего по одному из проводников. Вектор магнитной индукции, величина которого определена соотношением (1), перпендикулярен описанной выше базовой плоской поверхности. Рассчитаем величину магнитного потока через эту поверхность:

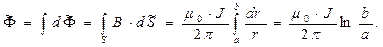(2)

Здесь волной над символом обозначена величина в пересчёте на единицу длины вдоль оси симметрии системы проводников. В соответствии с определением индуктивности находим индуктивность единицы длины коаксиального кабеля:

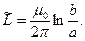(3)

С помощью именно этой физической величины описываются квазистационарные электромагнитные явления в протяженных коаксиальных кабелях (например, уравнения телеграфистов, рассмотренные в одном из следующих разделов курса).

6.9.3. Индуктивность двухпроводной линии.

Рассмотрим два прямолинейных достаточно тонких проводника круглого поперечного сечения радиуса , расположенных в пространстве параллельно друг другу так, что расстояние между осями их поперечных сечений равно 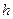, при этом выполнено условие 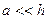(рис. 1). Пусть по левому проводнику ток 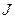течёт «от нас», а по правому проводнику тот же ток течёт «к нам». В силу оговоренного выше условия распределение тока по поперечным сечениям проводников можно считать равномерным. Индуктивность двухпроводной линии рассчитывается на единицу длины. Магнитный поток при этом пронизывает поверхность единичной длины, эта поверхность опирается на контур, показанный на рис. 1.

Начало оси абсцисс расположим посередине между проводниками. Координата 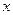при этом изменяется от значения –(h/2-a) до значения (h/2-a).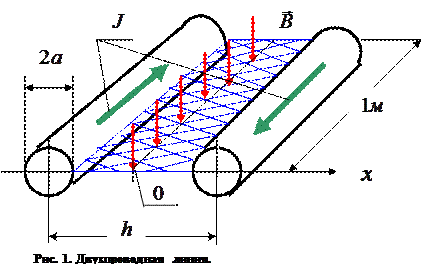

Величина магнитной индукции от левого проводника описывается выражением: (1)

а от правого проводника в той же точке пространства – выражением 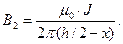(2)

Заметим, что векторы магнитной индукци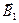и и 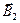параллельны друг другу и одинаково направлены для всех точек плоскости, проходящей через рассматриваемые проводники, если эти точки лежат между проводниками. В этом случае величина результирующего магнитного поля в рассматриваемой области изменения переменной 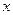является суммой величин 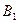и 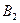. Вычислим результирующий магнитный поток через описанную выше поверхность:

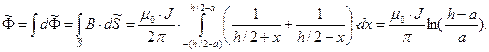(3)

Из соотношения (3) следует зависимость для погонной индуктивности двухпроводной линии при условии h>>a:

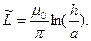(4)

Зависимость (4) оказывается эффективным параметром двухпроводной длинной линии, рассчитанная с её помощью величина скорости распространения электромагнитной волны вдоль двухпроводной линии совпадает с величиной скорости волны, измеренной экспериментально.