Наклонное падение плоской гармонической электромагнитной волны на границу раздела сред диэлектрик-проводник.
Целью настоящего раздела является описание явления отражения-преломления плоской однородной гармонической волны при её наклонном падении на плоскую границу раздела диэлектрической среды и проводящей среды. Необходимость вернуться к этому вопросу после рассмотрения формул Френеля для случая наклонного падения электромагнитной волны на границу раздела двух диэлектрических сред обусловлена некоторыми новыми специфическими закономерностями явления, которые возникают из-за того, что одна из сред является проводящей.
Переменное электромагнитное поле описывается системой уравнений Максвелла в дифференциальной форме, величины диэлектрической 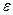 и магнитной
и магнитной 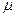 проницаемостей и удельной электропроводности
проницаемостей и удельной электропроводности 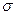 гипотетической (т.е. модельной) среды считаем независящими от времени и пространственных координат. В непроводящей среде (диэлектрик) выполняется условие
гипотетической (т.е. модельной) среды считаем независящими от времени и пространственных координат. В непроводящей среде (диэлектрик) выполняется условие 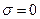 .
.
Решение системы уравнений Максвелла представляем в форме плоских гармонических бегущих волн:
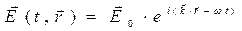 ,
, 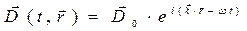
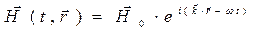 ,
, 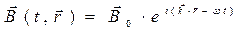 , (1)
, (1)
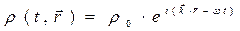
где 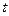 - текущее время,
- текущее время, 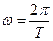 - круговая частота волны,
- круговая частота волны, 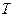 - период колебаний физической величины, принимающей участие в волновом процессе. Здесь
- период колебаний физической величины, принимающей участие в волновом процессе. Здесь 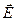 - вектор напряжённости электрического поля,
- вектор напряжённости электрического поля, 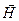 - вектор напряжённости магнитного поля,
- вектор напряжённости магнитного поля, 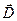 - вектор электрического смещения,
- вектор электрического смещения, 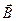 - вектор магнитной индукции,
- вектор магнитной индукции, 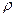 - объёмная плотность сторонних электрических зарядов. Предполагаем, как и прежде, что круговая частота
- объёмная плотность сторонних электрических зарядов. Предполагаем, как и прежде, что круговая частота 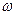 является вещественной постоянной скалярной величиной, а вектор
является вещественной постоянной скалярной величиной, а вектор 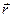 - радиус-вектором точки наблюдения. Волновой вектор ниже рассматриваем как вектор с комплексными компонентами:
- радиус-вектором точки наблюдения. Волновой вектор ниже рассматриваем как вектор с комплексными компонентами:
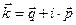 , (2)
, (2)
где отличные друг от друга по величине и направлению векторы 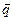 и
и 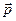 имеют вещественные компоненты.
имеют вещественные компоненты.
Векторные величины 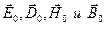 в соотношении (1) будем считать постоянными векторными величинами (амплитудами плоских гармонических волн). Результаты вычисления дивергенции и ротора векторных величин (1) были не один раз описаны в предыдущих разделах. Таким образом, система уравнений переменного гармонического электромагнитного поля, записанная для векторов напряжённости электрического и магнитного полей, формально приобретает «алгебраический» вид:
в соотношении (1) будем считать постоянными векторными величинами (амплитудами плоских гармонических волн). Результаты вычисления дивергенции и ротора векторных величин (1) были не один раз описаны в предыдущих разделах. Таким образом, система уравнений переменного гармонического электромагнитного поля, записанная для векторов напряжённости электрического и магнитного полей, формально приобретает «алгебраический» вид:
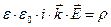 , (3)
, (3)
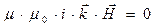 , (4)
, (4)
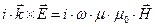 , (5)
, (5)
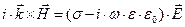 . (6)
. (6)
Из уравнений (5) и (6) следует, что должны быть выполнены условия «алгебраической ортогональности» векторов 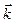 и
и 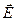 ,
, 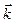 и
и 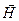 и
и 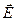 и
и 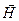 . Из уравнений (3) и (6) следует обращение в нуль объёмной плотности сторонних зарядов (
. Из уравнений (3) и (6) следует обращение в нуль объёмной плотности сторонних зарядов ( 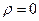 ).
).
Используя уравнение (5) как зависимость вектора напряжённости магнитного поля от вектора напряжённости электрического поля, из уравнения (6) получаем дисперсионное уравнение в форме:
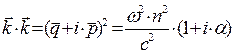 ,
, 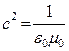 ,
, 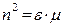 ,
, 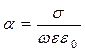 . (7)
. (7)
В дисперсионном уравнении (7) специально подчёркнут комплексный характер вектора 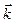 в проводящей среде, поскольку величина
в проводящей среде, поскольку величина 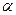 , пропорциональная проводимости среды, отлична от нуля. Разделяя действительную и мнимую части комплексного уравнения (7), получаем систему уравнений с действительными переменными:
, пропорциональная проводимости среды, отлична от нуля. Разделяя действительную и мнимую части комплексного уравнения (7), получаем систему уравнений с действительными переменными:
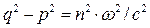 ,
, 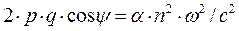 . (8)
. (8)
Угол 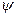 в системе уравнений (8) – угол между двумя действительными векторами
в системе уравнений (8) – угол между двумя действительными векторами 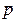 и
и 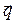 , величины p и q без стрелок над ними представляют собой модули соответствующих векторов. Решение системы уравнений (8), отвечающее физическому смыслу рассматриваемых величин, имеет вид:
, величины p и q без стрелок над ними представляют собой модули соответствующих векторов. Решение системы уравнений (8), отвечающее физическому смыслу рассматриваемых величин, имеет вид:
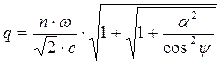 ,
, 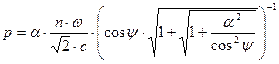 . (9)
. (9)
При необходимости в выражения (9) можно подставить параметры первой (непроводящей) или второй (проводящей) среды. В случае непроводящей среды параметр 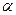 обращается в нуль, вместе с ним в нуль обращается и вектор
обращается в нуль, вместе с ним в нуль обращается и вектор 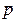 , волновой вектор
, волновой вектор 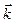 становится вектором с действительными компонентами.
становится вектором с действительными компонентами.
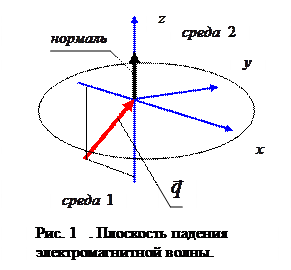 Ниже рассматриваем падение электромагнитной волны из диэлектрика (среда 1) в проводник (среда 2). В диэлектрике величина
Ниже рассматриваем падение электромагнитной волны из диэлектрика (среда 1) в проводник (среда 2). В диэлектрике величина 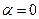 , поэтому волновой вектор
, поэтому волновой вектор 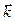 имеет только действительную составляющую, а его ориентация в пространстве определяется единственным образом – направлением вектора
имеет только действительную составляющую, а его ориентация в пространстве определяется единственным образом – направлением вектора 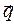 . Плоскость падения электромагнитной волны определяется вектором
. Плоскость падения электромагнитной волны определяется вектором 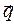 и нормалью к поверхности раздела, положительное направление нормали выбираем в сторону среды 2. Декартову систему координат удобно построить следующим образом. Ось z направим по направлению нормали, ось х расположим в плоскости падения, а ось у – перпендикулярно плоскости падения, причём направления соответствующих ортов
и нормалью к поверхности раздела, положительное направление нормали выбираем в сторону среды 2. Декартову систему координат удобно построить следующим образом. Ось z направим по направлению нормали, ось х расположим в плоскости падения, а ось у – перпендикулярно плоскости падения, причём направления соответствующих ортов 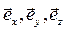 образуют правую систему координат.
образуют правую систему координат.
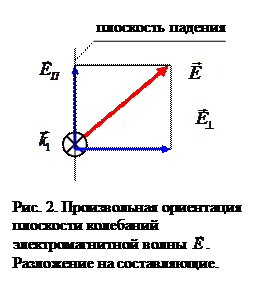 В линейной теории электромагнитного поля справедлив принцип суперпозиции. Это даёт нам право рассматривать по отдельности более простые случаи поляризации падающей электромагнитной волны. Рассмотрим рисунок 2. Пусть волновой вектор падающей волны перпендикулярен плоскости рисунка 2, вертикальная ось координат
В линейной теории электромагнитного поля справедлив принцип суперпозиции. Это даёт нам право рассматривать по отдельности более простые случаи поляризации падающей электромагнитной волны. Рассмотрим рисунок 2. Пусть волновой вектор падающей волны перпендикулярен плоскости рисунка 2, вертикальная ось координат
лежит в плоскости падения, а горизонтальная ось перпендикулярна плоскости падения. Произвольный вектор 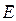 , перпендикулярный волновому вектору, можно разложить на две составляющие:
, перпендикулярный волновому вектору, можно разложить на две составляющие: 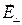 и
и 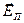 . Первую ориентацию плоскости колебаний электромагнитной волны называют S-поляризацией, вторую – P-поляризацией. Анализ S-поляризации электромагнитной волны несколько проще, чем анализ P-поляризации, поэтому сначала рассмотрим этот случай.
. Первую ориентацию плоскости колебаний электромагнитной волны называют S-поляризацией, вторую – P-поляризацией. Анализ S-поляризации электромагнитной волны несколько проще, чем анализ P-поляризации, поэтому сначала рассмотрим этот случай.
S-поляризация падающей электромагнитной волны –вектор напряжённости электрического поля направлен перпендикулярно плоскости падения электромагнитной волны (рис.3). Волновой вектор падающей волны опишем соотношениями:
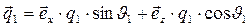 ,
, 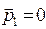 . (10)
. (10)
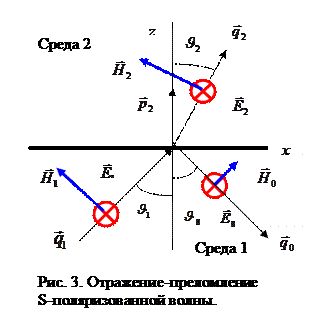 Здесь угол
Здесь угол 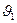 - острый угол между направлением волнового вектора
- острый угол между направлением волнового вектора 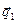 и направлением оси z,
и направлением оси z, 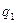 - модуль вектора
- модуль вектора 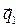 . С целью обеспечения перпендикулярности вектора напряженности электрического поля плоскости падения зададим эту векторную величину соотношением:
. С целью обеспечения перпендикулярности вектора напряженности электрического поля плоскости падения зададим эту векторную величину соотношением: 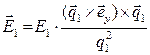 ,
, 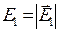 . (11)
. (11)
По символической форме записи (11) легко проверяется условие перпендикулярности колебаний вектора 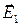 плоскости падения и взаимная ортогональность векторов
плоскости падения и взаимная ортогональность векторов 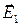 и
и 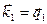 , а непосредственное вычисление его компонент приводит к зависимости:
, а непосредственное вычисление его компонент приводит к зависимости:
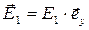 . (12)
. (12)
Воспользуемся уравнением (5) для формирования вектора напряжённости магнитного поля в падающей волне:
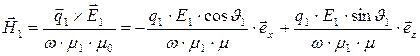 . (13)
. (13)
Легко видеть ( 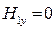 ), что вектор напряжённости магнитного поля падающей волны лежит в плоскости падения. Можно проверить, что вектор
), что вектор напряжённости магнитного поля падающей волны лежит в плоскости падения. Можно проверить, что вектор 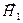 ортогонален волновому вектору
ортогонален волновому вектору 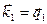 и ортогонален вектору
и ортогонален вектору 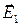 . Комплексный вектор Умова-Пойнтинга падающей волны направлен параллельно волновому вектору:
. Комплексный вектор Умова-Пойнтинга падающей волны направлен параллельно волновому вектору:
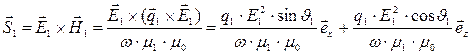 . (14)
. (14)
Волновой вектор отражённой волны (нижний индекс 0) опишем как вектор произвольной ориентации в пространстве, полагая только, что его направление составляет тупой угол с направлением нормали к поверхности раздела сред: 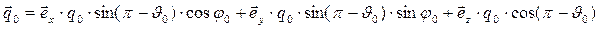 =
=
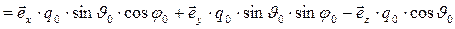 . (15)
. (15)
В выражении (15) угол 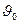 - угол отражения, а угол
- угол отражения, а угол 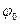 - угол между плоскостью падения и плоскостью отражения. Учитывая, что падающая волна и отражённая волна распространяются в одной и той же непроводящей среде, величину
- угол между плоскостью падения и плоскостью отражения. Учитывая, что падающая волна и отражённая волна распространяются в одной и той же непроводящей среде, величину 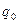 положим равной величине
положим равной величине 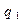 . В рассматриваемой ситуации должно иметь место условие периодического совместного изменения параметров и падающей и отражённой волны вдоль координаты х и координаты у. Из этого условия следует равенство проекций волновых векторов падающей и отражённой волн на соответствующие направления:
. В рассматриваемой ситуации должно иметь место условие периодического совместного изменения параметров и падающей и отражённой волны вдоль координаты х и координаты у. Из этого условия следует равенство проекций волновых векторов падающей и отражённой волн на соответствующие направления:
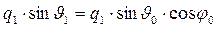 ,
, 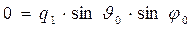 . (16)
. (16)
Единственным решением системы уравнений (16) является
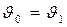 ,
, 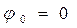 . (17)
. (17)
Примечательно, что таким образом получены геометрические условия отражения: угол падения равен углу отражения, волновой вектор отражённой волны лежит в плоскости падения:
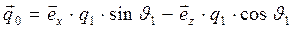 ,
, 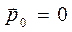 . (18)
. (18)
Условие «ортогональности» для отражённой волны будет выполнено, если
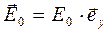 . (19)
. (19)
Форма решения для вектора напряжённости электрического поля в отражённой волне совпадает с аналогичным результатом (12) для падающей волны.
В соответствии с уравнением (5) выпишем выражение для вектора напряжённости магнитного поля в отражённой волне:
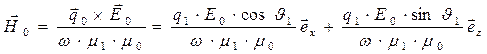 . (20)
. (20)
Этот вектор лежит в плоскости падения (множитель при 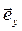 равен нулю). Комплексный вектор Умова-Пойнтинга для отражённой волны
равен нулю). Комплексный вектор Умова-Пойнтинга для отражённой волны
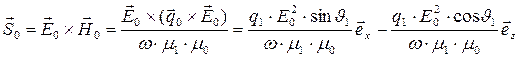 (21)
(21)
направлен параллельно волновому вектору 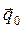 .
.
Переходим к рассмотрению электромагнитного поля в преломлённой волне. Она распространяется в проводящей среде, в этом случае волновой вектор 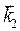 имеет действительную часть
имеет действительную часть 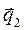 и мнимую часть
и мнимую часть 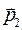 , модули описанных векторов определяются соотношениями (9).Произвольная пространственная ориентация этих векторов может быть описана выражениями:
, модули описанных векторов определяются соотношениями (9).Произвольная пространственная ориентация этих векторов может быть описана выражениями:
 , (22)
, (22)
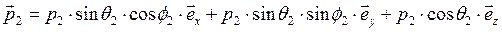 . (23)
. (23)
В выражениях (22) и (23) угол 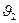 - угол преломления, а угол
- угол преломления, а угол 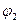 - угол между плоскостью падения и плоскостью «преломления», т.е. плоскостью, образованной вектором
- угол между плоскостью падения и плоскостью «преломления», т.е. плоскостью, образованной вектором 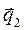 и нормалью к поверхности раздела. Углы
и нормалью к поверхности раздела. Углы 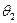 и
и 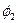 определяют пространственную ориентацию вектора
определяют пространственную ориентацию вектора 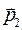 . Перечисленные величины углов подлежат определению.
. Перечисленные величины углов подлежат определению.
В рассматриваемой ситуации должно иметь место условие периодического совместного изменения параметров и падающей и преломлённой волны вдоль координаты х и вдоль координаты у. Из этого условия следуют условия равенства проекций комплексных волновых векторов падающей и преломлённой волн на соответствующие направления:
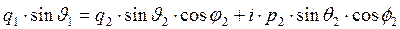 , (24)
, (24)
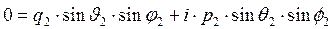 . (25)
. (25)
Уравнения (24)-(25) – комплексные, поэтому фактически имеют место четыре уравнения: два для действительных частей и два для мнимых частей системы (24)-(25). Решение этой системы имеет вид:
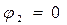 ,
, 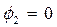 ,
, 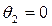 ,
, 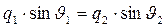 . (26)
. (26)
Оказывается, что действительная часть волнового вектора преломлённой волны лежит в плоскости падения, а его мнимая часть совпадает по направлению с направлением нормали к поверхности раздела сред, значение параметра 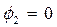 в этом случае значения не имеет. Последнее из соотношений (26) является обобщённым законом преломления Снеллиуса, который должен выполняться, если вторая среда является проводящей:
в этом случае значения не имеет. Последнее из соотношений (26) является обобщённым законом преломления Снеллиуса, который должен выполняться, если вторая среда является проводящей:
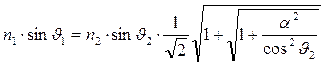 . (27)
. (27)
Если вторая среда является диэлектриком (параметр проводимости 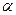 равен нулю), соотношение (27) переходит в классический закон преломления.
равен нулю), соотношение (27) переходит в классический закон преломления.
Все физические величины в соотношении (27)с точки зрения математики являются действительными величинами, значения 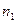 и
и 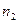 при этом определены зависимостями (7) через действительные значения диэлектрической и магнитной проницаемостей соответствующей среды. Заметим, что в рассматриваемом случае правая часть соотношения (27) зависит от величины круговой частоты
при этом определены зависимостями (7) через действительные значения диэлектрической и магнитной проницаемостей соответствующей среды. Заметим, что в рассматриваемом случае правая часть соотношения (27) зависит от величины круговой частоты 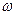 электромагнитной волны (7).
электромагнитной волны (7).
На рисунках 4 и 5 приведена графическая иллюстрация обобщённого закона Снеллиуса. На рисунке 4 приведены результаты расчётов величины угла преломления в зависимости от величины угла падения при заданном параметре проводимости второй среды и различных значениях относительного показателя преломления 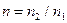 . С увеличением относительного показателя преломления вектор
. С увеличением относительного показателя преломления вектор 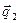 сильнее «прижимается» к направлению нормали. Это явление качественно совпадает с аналогичным явлением в случае отсутствия проводимости второй среды.
сильнее «прижимается» к направлению нормали. Это явление качественно совпадает с аналогичным явлением в случае отсутствия проводимости второй среды.
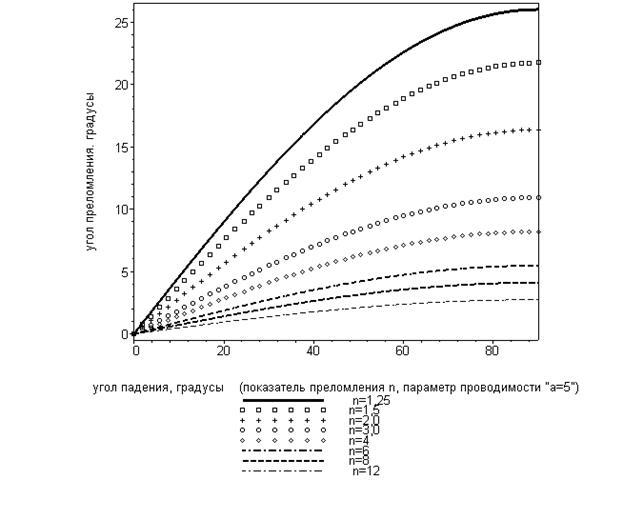
Рис.4. Зависимость величины угла преломления от угла падения при различных значениях относительного показателя преломления n.
На рисунке 5 приведены результаты расчётов величины угла преломления в зависимости от величины угла падения при заданном значении относительного показателя преломления 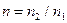 и нескольких значениях параметра проводимости второй среды. С увеличением параметра проводимости
и нескольких значениях параметра проводимости второй среды. С увеличением параметра проводимости 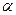 второй среды вектор
второй среды вектор 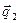 сильнее «прижимается» к направлению нормали. При очень большой проводимости второй среды угол преломления становится настолько малым, что преломлённая волна, кажется, распространяется по нормали к поверхности раздела. Эта особенность взаимодействия электромагнитной волны с хорошими проводниками лежит в основе приближённых граничных условий Леонтовича для электромагнитного поля.
сильнее «прижимается» к направлению нормали. При очень большой проводимости второй среды угол преломления становится настолько малым, что преломлённая волна, кажется, распространяется по нормали к поверхности раздела. Эта особенность взаимодействия электромагнитной волны с хорошими проводниками лежит в основе приближённых граничных условий Леонтовича для электромагнитного поля.
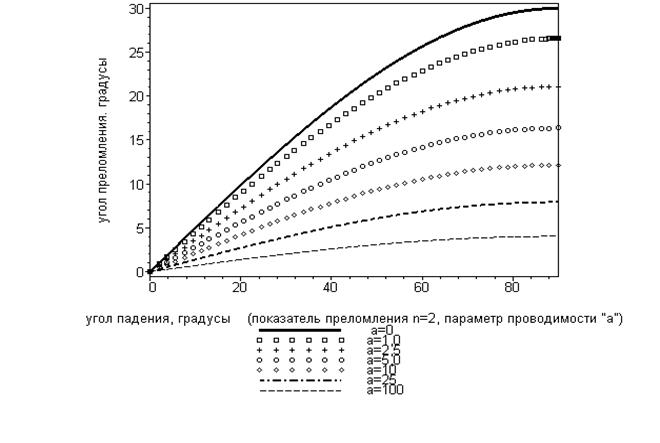
Рис.5. Зависимость величины угла преломления от угла падения при различных значениях 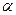 - параметра проводимости второй среды.
- параметра проводимости второй среды.
Итак, волновой вектор преломлённой среды можно считать определённым:
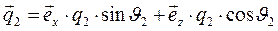 ,
, 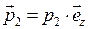 . (28)
. (28)
Модули векторов 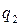 и
и 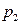 можно рассчитать по соотношениям (9), приняв во внимание условие
можно рассчитать по соотношениям (9), приняв во внимание условие 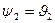 . Из определений (28) следует, что комплексный волновой вектор преломлённой волны лежит в плоскости падения (отсутствуют составляющие вдоль оси у).
. Из определений (28) следует, что комплексный волновой вектор преломлённой волны лежит в плоскости падения (отсутствуют составляющие вдоль оси у).
Условие «ортогональности» векторов 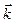 и
и 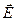 выполнено для структуры
выполнено для структуры 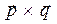 и для структуры
и для структуры 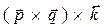 . Поскольку в падающей и отражённой волнах векторы напряжённости электрического поля имеют проекции только на ось у, а касательные компоненты напряжённости электрического поля при переходе через границу раздела сред должны совпадать, то, очевидно, что решение для преломлённой волны следует искать в форме первой структуры:
. Поскольку в падающей и отражённой волнах векторы напряжённости электрического поля имеют проекции только на ось у, а касательные компоненты напряжённости электрического поля при переходе через границу раздела сред должны совпадать, то, очевидно, что решение для преломлённой волны следует искать в форме первой структуры:
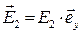 . (29)
. (29)
Используя принятую форму для вектора напряжённости электрического поля в преломлённой волне, запишем выражение для соответствующего вектора напряжённости магнитного поля:
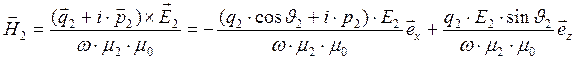 . (30)
. (30)
Для построенного решения легко проверяется условие ортогональности векторов 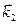 и
и 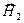 и
и 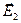 и
и 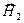 . Комплексный вектор Умова-Пойнтинга для преломлённой волны
. Комплексный вектор Умова-Пойнтинга для преломлённой волны
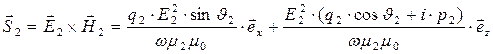 (31)
(31)
лежит в плоскости падения (отсутствует составляющая вдоль оси у) и направлен параллельно комплексному вектору 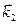 .
.
Перейдём к рассмотрению условий сопряжения электрического и магнитного полей на границе раздела двух сред. Условие непрерывности касательных компонент векторов напряжённости электрического поля вдоль оси х тривиально – все они равны нулю по построению решения. Условие непрерывности касательных компонент векторов напряжённости электрического поля вдоль оси у приводит к соотношению
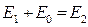 . (32)
. (32)
Условие непрерывности нормальных компонент векторов магнитной индукции при переходе через границу раздела
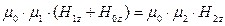 (33)
(33)
после подстановки соответствующих выражений и использования геометрических законов отражения-преломления приводится к уравнению (32) и не может вследствие этого рассматриваться как независимое уравнение для определения амплитуд искомых электрического и магнитного полей.
Структура электрических полей в падающей, отражённой и преломлённой волне не содержит нормальных к поверхности раздела компонент, поэтому можно предположить, что на границе раздела сред отсутствует поверхностная плотность стороннего электрического заряда, что согласуется с обращением в нуль нормальных компонент объёмной плотности тока проводимости по обе стороны от границы раздела сред.
Предположим дополнительно, что на поверхности раздела сред отсутствует и поверхностная плотность токов проводимости. В этом случае на поверхности раздела должны быть непрерывны касательные компоненты векторов напряжённости магнитного поля. В проекции на ось у это условие тривиально: таких компонент нет по построению решения. Рассматривая проекцию на ось х, приходим к уравнению
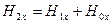 . (34)
. (34)
После подстановки в уравнение (34) соответствующих зависимостей, получаем: 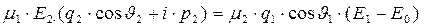 . (35)
. (35)
Итак, для нахождения двух неизвестных величин 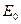 и
и 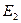 имеем систему двух уравнений (32) и (35). Решение этой системы имеет вид:
имеем систему двух уравнений (32) и (35). Решение этой системы имеет вид:
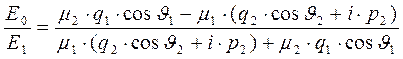 , (36)
, (36)
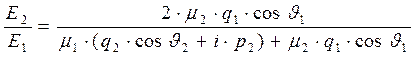 . (37)
. (37)
Правые части зависимостей содержат только известные или рассчитываемые предварительно величины. Расписывать их более подробно нецелесообразно ввиду громоздкости формы записи.
Располагая зависимостями (36) и (37), с помощью выражений (20) и (30) находим амплитуды колебаний векторов напряжённости магнитного поля соответственно в отражённой и преломлённой волне:
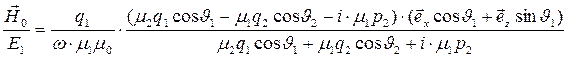 , (38)
, (38)
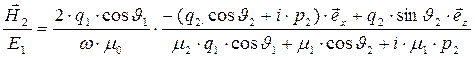 . (39)
. (39)
Решение можно считать законченным: построенные зависимости удовлетворяют уравнениям классической электродинамики в каждой среде и всем соотношениям на границе раздела, при этом на поверхности раздела нет поверхностной плотности сторонних зарядов и поверхностных токов проводимости. Условия непрерывности касательных компонент векторов напряжённости электрического и магнитного полей в отсутствие поверхностного тока проводимости использованы при построении решения, выполнение условия непрерывности нормальных компонент вектора магнитной индукции проверено. Условия скачка нормальных компонент вектора 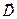 выполнены, если равна нулю поверхностная плотность сторонних электрических зарядов. Этот результат не противоречит закону сохранения электрического заряда на поверхности раздела диэлектрик-проводник, поскольку по постановке задачи равны нулю нормальные компоненты вектора объёмной плотности тока проводимости и отсутствует поверхностная плотность токов проводимости на границе раздела.
выполнены, если равна нулю поверхностная плотность сторонних электрических зарядов. Этот результат не противоречит закону сохранения электрического заряда на поверхности раздела диэлектрик-проводник, поскольку по постановке задачи равны нулю нормальные компоненты вектора объёмной плотности тока проводимости и отсутствует поверхностная плотность токов проводимости на границе раздела.
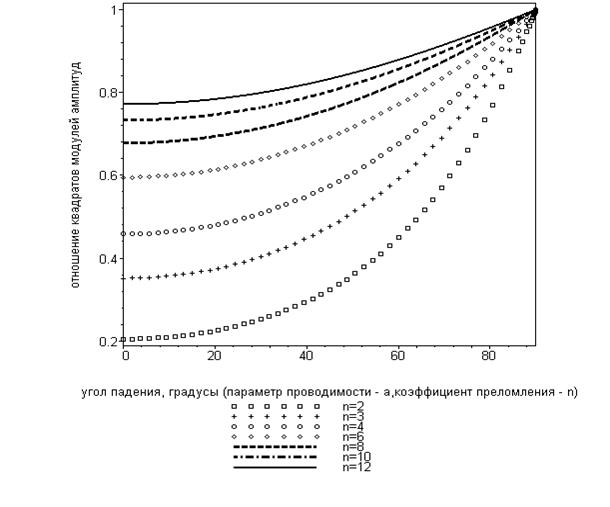
Рис. 6. Зависимость квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны S-поляризации (параметр проводимости 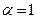 ).
).
На рис. 6 показано семейство кривых зависимости квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны S-поляризации для нескольких значений относительного показателя преломления 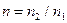 при заданной величине параметра проводимости
при заданной величине параметра проводимости 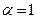 второй среды. Это отношение монотонно возрастает с увеличением угла падения электромагнитной волны и с увеличением относительного показателя преломления.
второй среды. Это отношение монотонно возрастает с увеличением угла падения электромагнитной волны и с увеличением относительного показателя преломления.
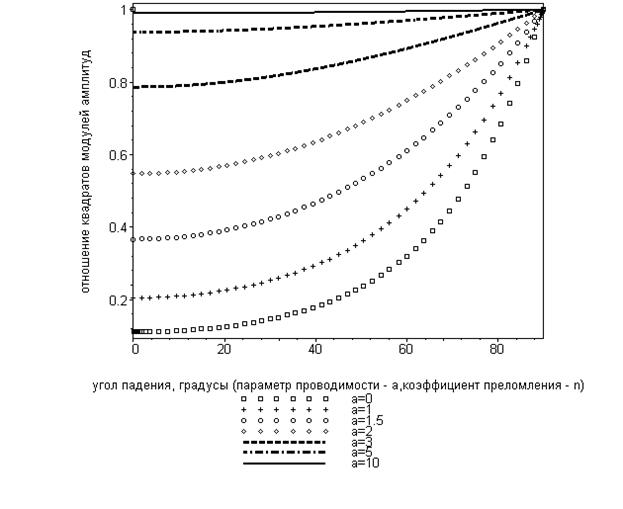
Рис.7. Зависимость квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны S-поляризации при различных значениях параметра проводимости и фиксированном значении относительного показателя преломления (n=2).
На рис.7 показано семейство кривых зависимости квадрата отношения модулей амплитуд векторов напряжённости электрического поля отражённой и падающей волны S-поляризации для нескольких значений параметра проводимости 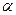 второй среды при заданной величине относительного показателя преломления
второй среды при заданной величине относительного показателя преломления 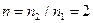 . Следует обратить внимание на монотонное увеличение степени отражения электромагнитной волны от поверхности раздела сред с увеличением параметра проводимости второй среды и возрастанием угла падения.
. Следует обратить внимание на монотонное увеличение степени отражения электромагнитной волны от поверхности раздела сред с увеличением параметра проводимости второй среды и возрастанием угла падения.
Дата добавления: 2017-09-01; просмотров: 2297;











