Критика научных представлений Френеля.

Состояние оптики в начале XIX века.

Со времени выдвижения принципа Фермá и принципа Гюйгенса прошло более ста лет. За это время наука, особенно механика, получила значительное развитие. Интенсивно развивалась и экспериментальная оптика. Вопрос о природе световых лучей оставался неразрешенным: теория Ньютона и теория Гюйгенса имели своих сторонников и своих противников.

Физические представления о природе световых волн в начале XIX века можно себе представить по письмам Томаса Юнга (1773-1829) – убеждённого сторонника Гюйгенса. В 1817 г. он писал: « Я размышлял о том, что невозможно дать совершенное объяснение влияния света, создающего поляризацию, если не отойти от классической теории волн. Принцип этой теории состоит в том, что все световые волны просто распространяются через однородные среды в виде концентрических сферических поверхностей как звуковые волны. Они просто состоят из прямых и обратных движений частиц в направлении радиуса с сопровождающими эти движения сгущениями и разрежениями. И тем не менее, в этой теории можно объяснить поперечные колебания, которые также распространяются в направлении радиуса и с равной скоростью, причём все частицы движутся в определённом направлении относительно этого радиуса; это и есть поляризация… Если мы примем тот факт, что поперечное движение может распространяться по прямой линии, как математический постулат в волновой теории, не пытаясь показать её физическую основу, мы сможем получить из этого допущения приемлемую иллюстрацию разделения поляризованного света при отражении в наклонной плоскости, допуская, что движение поляризованного света разлагается »… на две составляющие, которые при отражении ведут себя по-разному.

Формулы Френеля.

В 1823 г. французский физик, член Парижской АН Огюстен Жан Френельсущественно дополнил содержание законов отражения и преломления плоской световой волны на неподвижной плоской поверхности раздела двух сред. Эти результаты известны в физике как «формулы Френеля». Формулы Френеля устанавливают соотношения между амплитудами падающей, отражённой и преломлённой волн и позволяют теоретически вычислять такие характеристики взаимодействия световой волны с границей раздела двух сред как коэффициент отражения и коэффициент пропускания волны. Физические представления Френеля для своего времени оказались весьма плодотворными, хотя и небезупречными с позиций сегодняшней науки. Их поразительная наглядность и простота математического аппарата немало способствовали успеху в изучении оптических явлений.

Френель считал, что само существование световых волн обусловлено динамическими свойствами светоносного эфира. В те годы концепция «эфира» была распространённой научной гипотезой. Френель считал, что колебания, из которых состоит свет, перпендикулярны направлению распространения волны (гипотеза о поперечном характере световых волн). Он согласен с Т. Юнгом в том, что явления отражения и преломления вызваны разностью инерционных свойств светоносного эфира, заполняющего различные материальные среды. Одно из основных предположений Френеля состоит в том, что «инерция эфира» обратно пропорциональна квадрату скорости света в среде. На поверхности раздела двух сред геометрические смещения соседних молекул должны быть параллельны плоскости раздела и одинаковы в обеих средах (условие непрерывности касательных компонент смещения). Кроме того, на границе раздела сред должен выполняться закон сохранения энергии. Это условие формулируется так: поток энергии падающей волны через элемент поверхности раздела сред равен сумме потоков энергии отражённой и преломлённой волн через этот же элемент поверхности раздела сред. Заметим, что представления Френеля во многом являются механистическими. Ниже мы ещё вернёмся к анализу этих представлений, а пока рассмотрим его результаты.

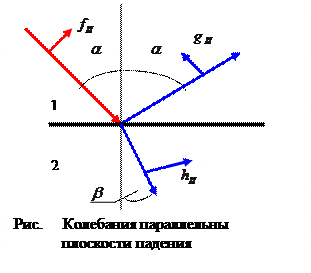
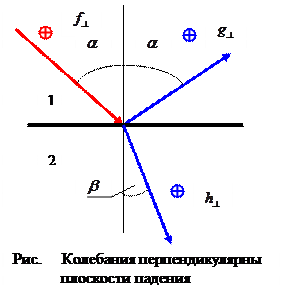Произвольные поперечные колебания эфира в световой волне можно разложить на колебания, перпендикулярные плоскости падения, и параллельные плоскости падения волны. Плоскость падения волны образована вектором направления распространения волны и вектором нормали к поверхности раздела сред. На рис. ???? плоскость падения является плоскостью рисунка. Удобно рассматривать по отдельности волны с первой и второй ориентацией направления колебаний, а результаты потом «сложить».

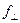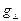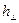Рассмотрим первый случай (рис. ). Пусть , и представляют собой амплитуды падающей, отражённой и преломлённой волн, угол падения 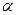равняется углу отражения, угол преломления обозначим величиной 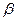. Световая волна падает из первой среды и преломляется во второй среде. Крестиками в кружках условно обозначены направления колебаний. В соответствии с представлениями Френеля плотность потоков энергии в каждой из волн пропорциональна выражениям:

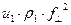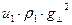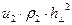, , . (1)

Здесь 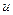- скорость волны, 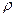- «инерция эфира». Плотность потока энергии в световой волне направлена вдоль соответствующего направления распространения волны. Запишем условие энергетического баланса для единичного элемента поверхности раздела сред и условие непрерывности касательных компонент смещения:

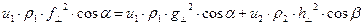, (2)

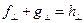. (3)

Дополним рассматриваемую математическую модель явления законом Снеллиуса

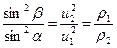. (4)

Из системы уравнений (2)-(4) получаются следующие зависимости:

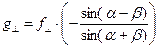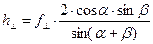, . (5)

В соответствии с полученными результатами колебания в преломлённой волне всегда совпадают по фазе с колебаниями в падающей волне, а фаза колебаний в отражённой волне испытывает скачок на величину полупериода, если вторая среда является оптически более плотной, и не испытывает скачка, если вторая среда является оптически менее плотной.

Рассмотрим второй случай: колебания в падающей, отражённой и преломлённой волнах происходят в направлении, параллельном плоскости падения волны (рис. ).

Плотности потоков энергии для рассматриваемых волн теперь описываются выражениями:

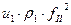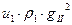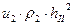, , . (6)

Баланс потоков энергии при переходе через границу раздела приобретает вид:

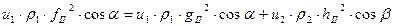. (7)

Условие непрерывности касательных составляющих смещения записывается в форме:

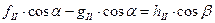. (8)

В дополнение к уравнениям (7) и (8) остаётся справедливым и уравнение (4).

Решение системы уравнений (7)-(8) и (4) приводит к соотношению:

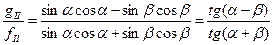. (9)

Соотношение (9) известно в оптике как закон тангенсов Френеля. Для амплитуды преломлённой волны получается соотношение:

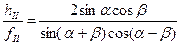. (10)

В случае нормального падения световой волны на плоскую границу раздела двух сред формулы Френеля значительно упрощаются. С помощью предельного перехода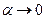

(при этом, естественно, и 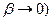получаем для абсолютных величин амплитуд колебаний в падающей, отражённой и преломлённой волн произвольной поляризации:

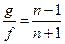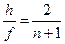, . (11)

Здесь 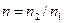- относительный показатель преломления. Наличие отражённой световой волны можно рассматривать как «потери» светового потока при прохождении границы раздела двух сред. Примечательно, что при переходе световой волны из воздуха в стекло ( 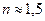) амплитуда отражённой волны составляет 0,2 от амплитуды падающей волны, а интенсивность, которая пропорциональна квадрату амплитуды, – всего 4% от интенсивности падающей волны. Практический вывод из этого результата: просветляющая плёнка на поверхности очков мало эффективна и практически бесполезна, заметный положительный эффект достигается только в сложных оптических многолинзовых системах при исследовании слабо светящихся объектов.

Из теории Френеля следует интересное явление, открытое экспериментально ещё в 1815 г. Дэвидом Брюстером (1781-1868). Оказывается, что при выполнении условия 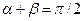(угол падения при этом называют углом Брюстера) амплитуда отражённой волны 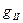обращается в нуль. Если в исходной падающей волне имели место колебания, параллельные плоскости падения и перпендикулярные ей, то в отражённой волне остались только колебания, направление которых перпендикулярно плоскости падения: из произвольной световой волны получилась плоско поляризованная световая волна.

Интересно, что Брюстер (член Лондонского Королевского общества и президент Эдинбургского Королевского общества) в своё время был больше известен как изобретатель калейдоскопа, чем своими работами в области кристаллооптики.

Критика научных представлений Френеля.

Многие современники Френеля не были согласны с представлениями Френеля. Среди них были весьма известные учёные. Лаплас, Био и Пуассон были убеждёнными сторонниками ньютоновской теории света. Даже Араго – первоначально сторонник Френеля – отказался принять гипотезу о поперечности световых волн. Механическая модель света Френеля постулировала существование эфира, заполняющего всё пространство и обладающего разными свойствами в различных телах. Два главных параметра эфира – «жесткость» и «свойство инерционности» обуславливали существование и природу световых волн. Во многом эти представления были похожи на теорию звуковых волн в газах и жидкостях и теорию продольных волн в твердых стержнях. Но звуковые волны в газах и жидкостях являются продольными волнами, а в твердых телах распространяются как продольные волны сжатия-разрежения, так и поперечные сдвиговые волны. Френель в 1821 г. принял гипотезу о поперечности световых волн: «Лишь несколько месяцев тому назад, размышляя с бóльшим вниманием по этому поводу, я признал весьма вероятным, что колебательные движения световых волн осуществляются только в плоскости волн как для простого, так и для поляризованного света…Я постараюсь показать, что гипотеза, которую я представляю, не содержит ничего физически невозможного и что она уже может служить для объяснения основных свойств поляризованного света». В теории Френеля все сложнейшие явления поляризации интерпретируются в удивительном согласии с экспериментальными данными и предстают как частные случаи общего закона сложения и разложения скоростей.

Но за этой гипотезой стоит предположение, что эфир – это твёрдая субстанция с очень большой «жесткостью» и очень малой плотностью, скорость волны в таком эфире равна скорости света, т.е. очень большой величине, а самое главное – в таком эфире принципиально не существуют продольные волны! По гипотезе Френеля «жёсткость» эфира одинакова во всех средах, а плотность его меняется в зависимости от того, какую среду он заполняет.

Физики в течение почти целого столетия пытались обосновать или опровергнуть гипотезу Френеля. На этом пути Франц Нейман (1798-1871) показал, что результаты Френеля можно получить, полагая, что плотность эфира постоянна во всех среда, а меняется его «жёсткость», а несколько позже Джон Уильям Рэлей (1842-1919) получил результаты Френеля в предположении, что в различных средах различны и «жёсткость» и плотность эфира. Возникает вопрос, каков же эфир на самом деле?

Другое направление исследований было связано с попыткой разработать механическую модель твёрдого тела с необходимыми свойствами. Заметим, что современникам Френеля был известен закон Гука в элементарной форме. Динамические уравнения теории упругости в трёхмерном пространстве (Клод-Луи-Мари-Анри Навье (1785-1836), Огюстен Луи Коши 91789-1857), Джордж Грин (1793-1841) и др.) в различных вариантах находились ещё в стадии разработок. Основной трудностью при этом оставалось то, что в упругом теле имеют место и продольные волны, а поперечная волна на границе раздела двух упругих сред порождает не только поперечную, но и продольную волну. Исключение продольных волн требовало принятия дополнительных физически трудно объяснимых гипотез. Условия Френеля на границе раздела сред с точки зрения теории упругости не являются замкнутыми: непрерывность касательных смещений постулируется, непрерывность силовых характеристик игнорируется.

Некоторые сторонники представлений Френеля даже после его смерти не претендовали на окончательное объяснение природы световых волн и осознавали недостаточность физической строгости выдвигаемой теории. Так Джеймс МакКулаг (1809-1847) в 1838 г. писал: «Если нас спросят, какими причинами можно обосновать гипотезы, на которых основана предшествующая теория, мы не сумеем дать удовлетворительный ответ. Мы вынуждены признать, что за исключением закона кинетической энергии, гипотезы ─ это всего лишь удачные догадки. Весьма вероятно, что эти догадки правильны, так как они привели к изящным законам, которые полностью подтверждаются на практике; но это всё, что мы можем утверждать о них. Мы не можем пытаться вывести их из первых принципов, потому что в теории света такие принципы ещё нужно найти. Несомненно, что свет производится волнами, которые распространяются с поперечными колебаниями через высокоупругий эфир; но строение этого эфира и законы его связи (если таковая существует) с частицами тел неизвестны».

В связи с проблемой существования светоносного эфира интересно замечание Джорджа Габриэля Стокса (1819-1903) о том, что планеты, двигаясь по орбитам с большими скоростями, должны испытывать ощутимое сопротивление. Сам Стокс предположил, что эфир подобен среде, которая ведёт себя как твердое тело при «быстрых» колебаниях и как жидкость поддаётся «медленном» воздействию планет. Сам Френель считал, что планета в своём движении увлекает окружающий её эфир, и даже определил «коэффициент увлечения эфира».

Собирая всё перечисленное вместе, трудно поверить, что существует субстанция с такими противоречивыми физическими свойствами.

Ради полноты обсуждения представлений Френеля заметим, что идея поперечности световых волн в зачаточном варианте высказана ещё Робертом Гуком (1635-1703): ему принадлежит демонстрация явления распространения поперечных колебаний вдоль верёвки, возбуждаемых периодическими поперечными смещениями одного из её концов. Особенно красиво подобное явление используется в художественной гимнастике – упражнение с лентой. Опыты с поляризованными лучами натолкнули в 1815 г. Андре Мари Ампера (1775-1836) на идею поперечности световых волн, который сообщил её Френелю. Прошло 6 лет, прежде чем Френель «поверил» в эту идею и стал её сторонником и основным разработчиком (по другим источникам Т. Юнг в письме к Д.Ф. Араго (1786-1853) провёл в 1818 г аналогию между поперечными световыми волнами и волнообразным движением верёвки, последний сообщил об этом Френелю, хотя сам эту концепцию не поддерживал).

В конце XIX века после создания законченной теории классической электродинамики Дж. К. Максвеллом вопрос о природе световых волн был полностью решён, а после работ А. Эйнштейна не стало необходимости вводить само понятие эфира.