АЦП последовательных приближений (Кодоимпульсный АЦП).

Схема АЦП последовательных приближений. (Рис. 13)

АЦП подобна выше рассмотренной. Однако вместо счетчика СТ использу­ется регистр RG последовательных приближений.

Работа АЦП последовательных приближений.

Регистр вначале в старший раз­ряд засылает "1"(разряд с весом 8).

Результат операции 1000 поступает через ЦАП на вход компаратора. Если входное напряжение U_вх больше напряжения на выходе ЦАП (U_вх>U_ЦАП) "1"оста­ётся в разряде и в регистр RG засылает "1" в разряд с весом 4.

Если входное напряжение U_вх меньше напряжения на выходе ЦАП (U_вх<U_ЦАП),то старший разряд обнуляется, а логическая единица вновь засылается в разряд с весом 4 и т.д.

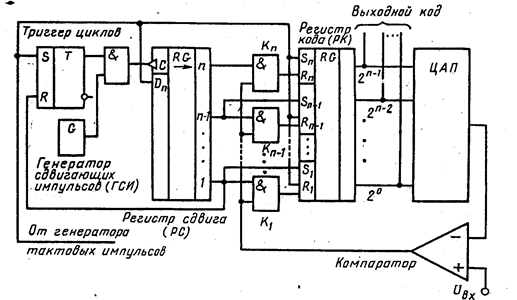
Рис. 13 АЦП последовательных приближений

Т.е. регистр RG "задаёт вопрос" больше или меньше цифровой код подаваемый на ЦАП входного напряжения U_вх, а компаратор отвечает на него.

Достоинствами схемы является:

* высокое быстродействие;

* можно увеличить разрядность кода при удовлетворительном быстродейс­твии, что приводит к увеличению точности преобразования.

В связи с этим, АЦП последовательных приближений наиболее широко распространены.

Параметры АЦП.

- диапазон изменения преобразуемой амплитуды входного напряжения;

- разрядность выходного двоичного кода;

- погрешность квантования преобразуемой величины;

- быстродействие, характеризуемое временем преобразования Т_пр входной величины

Применение АЦП и ЦАП.

1) Основное назначение АЦП и ЦАП - сопряжение аналоговых и цифровых уст­ройств друг с другом в системах сбора, передачи и обработки информации.

2) Для построения линий цифровой связи.

3) Для создания гибридных вычислительных машин.

4) В РПУ Р-719 (в блоке П-111 – частотном селекторе). Здесь применяется АЦП последовательных приближений (кодоимпульсные преобразователи), который преобразует амплитуду в код уровня.

Таким образом, наибольшее распространение получили кодоимпульсные преобразователи.

Заключение:

1. Для преобразования аналогового сигнала в цифровую форму и наоборот служат АЦП и ЦАП.

2. Наибольшее применение получили

· ЦАП с резистивной матрицей;

· АЦП последовательных приближений;

· АЦП временного преобразования.