Переходные процессы в длинных линиях.

Длинными линиями называются электрические системы, образованные двумя проводящими поверхностями, поперечные размеры таких систем значительно меньше, чем продольный размер. Примерами длинных линий могут служить двухпроводная линия и коаксиальный кабель (рис. 1).

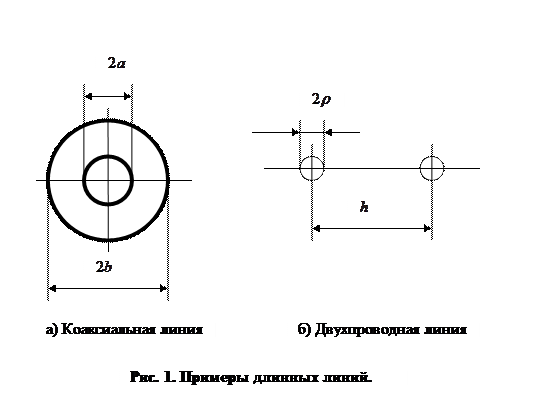
В общем случае нестационарное электромагнитное поле в рассматриваемых системах определяется фундаментальными уравнениями электродинамики (система уравнений Максвелла). В длинных линиях могут существовать волны, у которых продольные компоненты векторов напряженностей электрического и магнитного полей равны нулю, а поперечные компоненты указанных полей зависят от поперечных координат, причем поле максимально у проводника и убывает в радиальном направлении при удалении от длинной линии. Волны такого типа называют волнами ТЕМ. Особенностью структуры волн ТЕМ в длинных линиях, когда расстояние между проводниками меньше длины волны, является то, что распределение поперечных компонент электрического поля в каждый данный момент времени совпадают с распределением компонент электростатического поля, т.е. с распределением поля в конденсаторе соответствующей формы. Напомним, что обкладки конденсатора имеют равный по величине и различный по знаку электрический заряд. Поперечные компоненты магнитного поля в волне ТЕМ в каждый момент времени совпадают с распределением напряженности стационарного магнитного поля, образованного равными по величине и противоположными по направлению токами, текущими вдоль проводов. При изучении длинных линий обычно делают предположение о том, что проводники имеют малое поперечное сечение, что даёт право не рассматривать действительное распределение тока по проводнику или считать его равномерным. Расчётная схема процессов, протекающих в двухпроводной линии, показана на рис. 2.

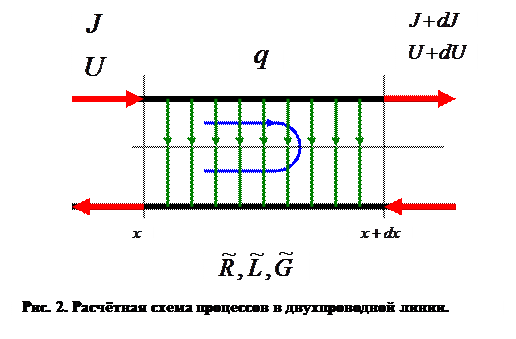
Погонная плотность электрического заряда 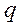(величина заряда обкладки конденсатора, приходящегося на единицу длины в продольном направлении 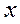) связана с током 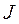, текущим по проводнику, уравнением непрерывности (закон сохранения электрического заряда):

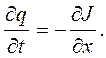(1)

Разность потенциалов между обкладками конденсатора определяется зависимостью:

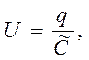(2)

где 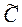- ёмкость конденсатора соответствующей формы в пересчёте на единицу длины. Если рассматриваемый параметр длинной линии в каждом поперечном сечении не зависит от времени, то из соотношения (2) следует «динамическое» уравнение:

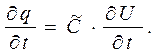(3)

Уравнения (1) и (3) позволяют связать между собой ток в проводнике и напряжение между проводниками:

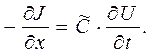(4)

В более общем случае в уравнении (4) можно учесть утечку электрического заряда, если ввести в рассмотрение погонную проводимость 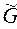пространства между проводниками (проводимость, определяемую для единицы длины системы) как коэффициент пропорциональности между током утечки на единице длины и напряжением между проводниками:

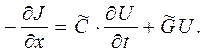(5)

Помимо закона сохранения электрического заряда в дифференциальной форме (5) необходимо включить в рассмотрение обобщённый закон Ома для участка цепи длиной :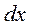

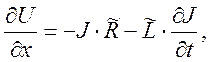(6)

где 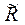- погонное сопротивление проводника (сопротивление единицы длины проводника), 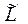- погонная индуктивность системы (индуктивность в расчёте на единицу длины).

Совокупность дифференциальных уравнений первого порядка в частных производных (5) и (6) называют «телеграфными уравнениями», они впервые были использованы при расчётах трансатлантического кабеля, соединившего Европу и Америку телеграфной линией связи.

Если из системы уравнений (5) и (6) исключить, например, силу тока 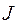, то получим уравнение в частных производных второго порядка относительно величины :

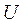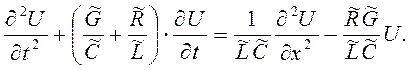(7)

Выяснение физического содержания уравнения (7) удобнее провести при рассмотрении идеальной длинной линии, в которой отсутствует погонное сопротивление 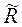и погонная проводимость утечки :

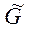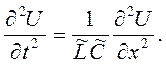(8)

Уравнением (8) описывается волна, распространяющаяся вдоль проводников. Скорость распространения волны определяется соотношением:

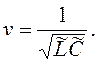(9)

Например, для двухпроводной линии в вакууме, для которой параметры длинной линии, т.е. величина емкости и величина индуктивности в пересчете на единицу длины, известны (раздел 4.7.4 зависимость 4 и раздел 6.9.3 зависимость 4), имеем

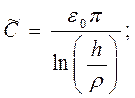
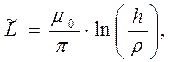(10)

откуда

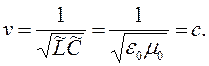(11)

Длинная линия, в отличие от рассмотренных выше электрических схем с сосредоточенными параметрами (динамика таких схем описывается уравнениями с обыкновенными производными) является системой с распределенными параметрами, её динамика описывается дифференциальными уравнениями с частными производными. Исследование подобных систем значительно сложнее, чем систем с сосредоточенными параметрами. С теорией волновых процессов мы познакомимся в одном из последующих томов курса. Математические вопросы, связанные с решением волновых уравнений, рассматриваются в руководствах по математической физике.