Последовательный RLC-контур.

Рассмотрим контур, состоящий из последовательно соединенных активного сопротивления R, конденсатора ёмкостью C и катушки индуктивности L (рис.1). Пусть положительное направление обхода контура и положительное направление тока совпадают между собой и направлены по часовой стрелке. Пусть положительный заряд q находится на верхней пластине конденсатора. Пусть к входным клеммам контура приложено переменное во времени входное напряжение 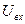, а также известно состояние рассматриваемого контура в начальный момент времени: значение тока в контуре и заряд конденсатора.

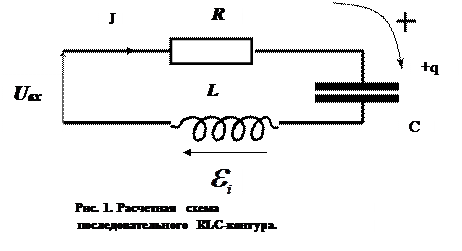
Для выбранного положительного направления обхода контура, положительного направления силы тока 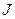и положительной полярности обкладок конденсатора имеют место следующие соотношения:

- закон сохранения электрического заряда

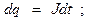(1)

- падение напряжения на обкладках конденсатора

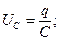(2)

- закон электромагнитной индукции

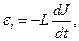
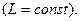(3)

Уравнение второго закона Кирхгофа для рассматриваемого контура в произвольный момент времени 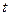имеет вид

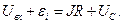(4)

Использование соотношений (1)-(3) в уравнении (4) приводит к следующему результату:

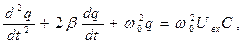
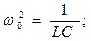
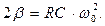(5)

Ниже ограничимся исследованием случая 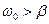, который имеет наибольшее практическое применение.

При произвольной зависимости входного напряжения от времени ( 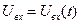) общее решение уравнения (5) может быть получено с помощью метода вариации произвольных постоянных, или с помощью интегрального преобразования Лапласа или с помощью какого-либо иного метода:

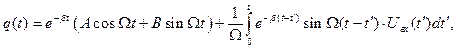(6)

где 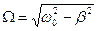. Для определения значений произвольных постоянных 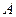и 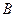требуется два дополнительных условия. Например, динамика процесса в рассматриваемом контуре полностью определена, если в начальный момент времени известна величина электрического заряда конденсатора 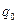и величина силы тока 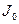. В отдельных случаях можно воспользоваться следующей формой записи общего решения дифференциального уравнения (5):

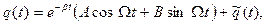(7)

где 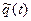- частное решение неоднородного уравнения (5). В произвольном случае угадать частное решение практически невозможно. Ниже рассмотрим динамические процессы в последовательной RLC-цепочке для случаев короткого замыкания входных клемм контура ( 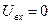), включения постоянного при 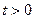входного напряжения ( 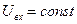) и гармонического колебания входного напряжения в режиме установившихся колебаний.

Режим короткого замыкания. В этом случае 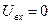, 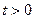. Если в начальный момент времени 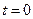электрический заряд обкладок конденсатора имел величину 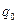, а сила тока в контуре составляла величину 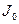, то динамика процессов, происходящих в контуре, описывается соотношениями:

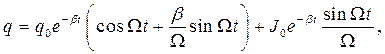(8)

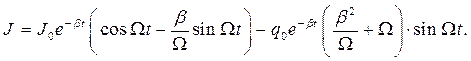( 9)

Соотношения (8)-(9) описывают затухающие гармонические колебания. Интересно отметить два обстоятельства. Первое, величина 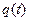не обращается в нуль, если в начальный момент времени электрический заряд на обкладках конденсатора равен нулю ( 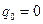). Аналогичное заключение можно сделать и относительно зависимости для силы тока 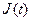в контуре. Только при одновременном выполнении услови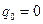й и 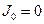имеют место соотношения 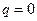и 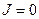, 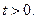Второе. Положительная, пусть малая по величине постоянная 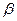обуславливает затухающий характер колебаний электрических величин в контуре. При условии 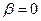соотношения (8) и (9) принимают вид:

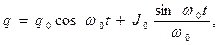(10)

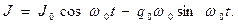(11)

Физический смысл соотношений (10)-(11) состоит в следующем. В идеальном RLC-контуре с последовательным соединением элементов в отсутствие активного сопротивления ( 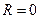) возможны незатухающие гармонические колебания с частотой 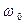. Период этих колебаний описывается формулой Томсона:

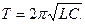(12)

Описанные колебания отсутствуют, если в момент короткого замыкания входных клемм контура заряд конденсатора 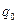был равен нулю (т.е. конденсатор был не заряжен) и в контуре не было электрического тока ( ).

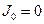Режим подключения контура к источнику постоянного напряжения. Этот режим характеризуется зависимостью 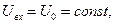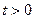при произвольных значениях величин электрического заряда на обкладках конденсатора и силы тока в цепи в начальный момент времени. С использованием формы (7) решения уравнения (5) можно получить:

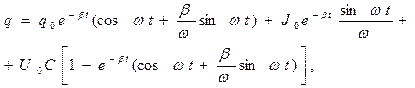(13)

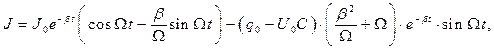(14)

где ,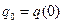

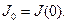
При стремлении переменной 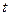к бесконечности имеет место постепенное затухание колебаний электрических величин в контуре и установление постоянных значений заряда конденсатора и величины силы тока:

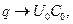
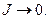(15)

Второе из соотношений (15) является следствием известного свойства конденсатора, конденсатор не проводит ток в цепи постоянного тока, поскольку его заряд не меняется с течением времени.

Полученные результаты справедливы при условии 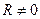. Если в соотношениях (13) и (14) вычислить предел при 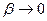(т.е. рассмотреть идеальный контур в отсутствие активного сопротивления 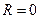), получим следующее:

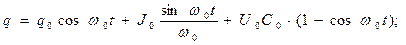(16)

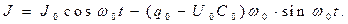(17)

Интересна структура зависимостей (16) и (17). При подключении контура к источнику постоянного напряжения в контуре имеют место незатухающие колебания, вызванные отличными от нуля начальными значениями заряда конденсатора и силы тока в цепи, и колебания, вызванные внешним воздействием. Анализ последних удобно провести при рассмотрении процесса «при нулевых начальных условиях» (на обкладках конденсатора нет электрического заряда и в цепи отсутствует электрический ток):

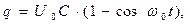(18)

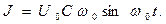(19)

Физический смысл соотношений (18)-(19) состоит в том, что в рассматриваемом режиме работы идеального LC-контура ( 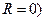с последовательным соединением элементов включенное в начальный момент времени постоянное напряжение на входных клеммах контура генерирует гармонические незатухающие колебания заряда конденсатора вокруг статического значения с амплитудой, равной статическому значению заряда конденсатора, и колебания силы электрического тока. Фаза колебаний тока при этом отличается от фазы колебаний заряда конденсатора на величину .

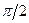Работа RLC-цепочки с последовательным соединением элементов в цепи переменного тока. Ниже рассмотрим динамические процессы в RLC-цепочке с последовательным соединением элементов при подсоединении её входных клемм к источнику переменного напряжения, свойства которого описываются зависимостью вида:

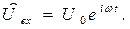(20)

Напомним, что физическое содержание условно будем приписывать действительной части зависимости (20). Заметим также, что ниже величина 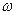представляет собой круговую частоту вынуждающего воздействия.

Допустим, что контур рассматривается в моменты времени, достаточно большие, чтобы имелась возможность пренебречь влиянием начальных значений физических величин в элементах контура вследствие эффекта затухания. Другими словами говоря, рассмотрим процесс установившихся колебаний, или, как говорят математики, рассмотрим задачу без начальных условий. В этом случае решение уравнения (5) можно искать в виде:

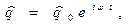(21)

где 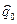- комплексная амплитуда гармонических колебаний электрического заряда на обкладках конденсатора. Подставим предполагаемое решение (21) в уравнение (5), сократим обе части полученного алгебраического соотношения на экспоненциальный сомножитель и получим зависимость:

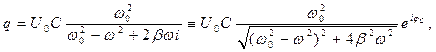(22)

где

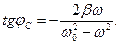(23)

Нижний индекс у величины 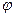следовало бы писать 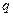, но поскольку ёмкость конденсатора является действительной положительной величиной, то для соответствующей величины начальной фазы колебаний падения напряжения на обкладках конденсатора выражение (23) оказывается справедливым и более удобным.

Соотношения (22)-(23) позволяют последовательно рассчитать мгновенные значения падения напряжения на обкладках конденсатора

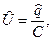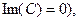( (24)

силы тока в цепи

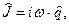(25)

падение напряжения на активном сопротивлении

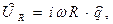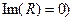( (26)

и падение напряжения на индуктивности 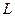(величина, обратная по знаку ЭДС электромагнитной индукции):

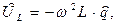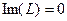( ). (27)

Легко проверить, что второй закон Кирхгофа для комплексных амплитуд, следовательно, и для мгновенных значений падений напряжения и ЭДС выполняется:

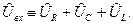(28)

Соотношение (28) служит для проверки правильности вычислений, не более того: вывод уравнения (5) был основан на использовании второго закона Кирхгофа для мгновенных значений упомянутых величин.

Формулой (23) определена величина отклонения фазы колебаний падения напряжения на обкладках конденсатора относительно фазы колебаний входного напряжения. Аналогичные результаты можно получить для начальных фаз колебаний падения напряжения на активном сопротивлении 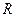и на индуктивности :

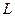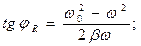
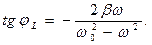(29)

Легко видеть, что для рассматриваемых величин выполнены равенства

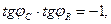
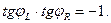(30)

Следствием равенств (30) является то, что на векторной диаграмме векторы 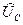и 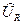взаимно перпендикулярны, а векторы 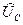и 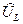параллельны друг другу. Прямое сравнение действительных и мнимых составляющих комплексных величин 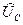и 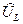позволяет установить, что они направлены вдоль одной прямой линии в противоположные стороны.

Представляет интерес рассмотреть «действующие» величины падений напряжения в RLC-цепочке с последовательным соединением элементов:

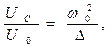
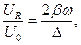
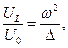(31)

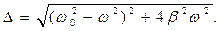
Соотношения (31) приведены на рис. 2 в форме графиков соответствующих зависимостей от отношения 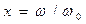при достаточно большом значении параметра 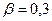(относительно большое активное сопротивление 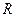в контуре).

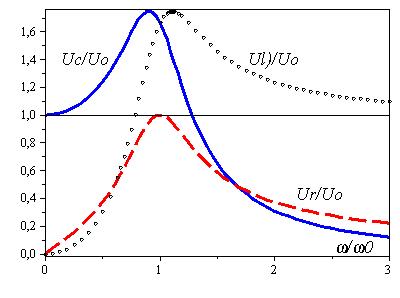
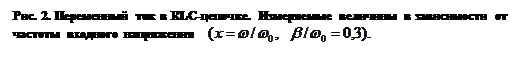
Обращает на себя внимание, что максимальные значения рассматриваемых падений напряжений как функции круговой частоты вынуждающего воздействия имеют место при различных значениях величины :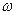

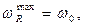
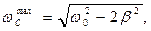
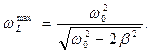(32)

При уменьшении параметра 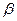это различие становится менее ощутимым и исчезает совсем, если рассматривается идеальный контур без активного сопротивления.

Если круговая частота 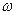вынуждающего воздействия совпадает с круговой частотой 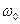, то падение напряжения на обкладках конденсатора и падение напряжения на индуктивности компенсируют друг друга, при этом падение напряжения на активном сопротивлении становится равным входному напряжению и совпадает с ним по фазе колебаний. А величина силы тока в цепи становится максимальной. В этом случае говорят о «резонансе напряжений». Явление резонанса напряжений имеет большое практическое значение.