Интеграл Лебега от простой функции

Числовая функция 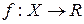, заданная на измеримом пространстве 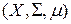с конечной мерой m, называется простой, если она принимает конечное или счётное число различных значений и является измеримой.

Теорема 1.Функция f является простой тогда и только тогда, когда 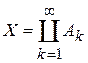, где множества 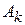измеримы и 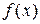принимает постоянное значение 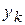на множестве 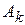, k=1,2,¼.

Теорема 2.Для любой измеримой функции 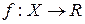, заданной на измеримом пространстве (X,S,m) существует последовательность 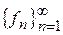простых функций, сходящаяся к 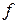в каждой точке x. Если функция f ограничена на X, то последовательность 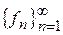можно выбрать равномерно сходящейся. Если 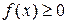, то можно выбрать 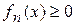так, чтобы последовательность 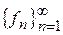была неубывающей.

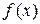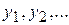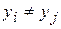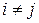Пусть – простая функция, принимающая значения , при . Обозначим через 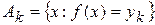, тогда .

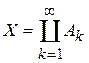Функция f называется интегрируемой по Лебегу, если ряд 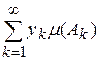сходится абсолютно. Если функция f интегрируема, то сумма этого ряда называется интегралом Лебега функции f, т.е.

.

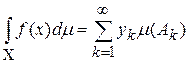Теорема.Пусть 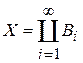и пусть на каждом B_i функция f принимает значение 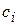. Тогда

,

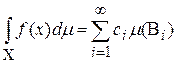причём функция f интегрируема на X тогда и только тогда, когда ряд сходится абсолютно.