Цикл Карно и его к.п.д. для идеального газа

Основываясь на втором начале термодинамики, Н. Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T₁) и холодильников (T₂), наибольшим к.п.д. обладают обратимые машины; при этом к.п.д. обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от конструкции машины.

Цикл, изученный Карно, является самым экономичным и представляет собой круговой процесс, состоящий из двух изотерм и двух адиабат. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем. Определим его к.п.д.

Цикл Карно схематически изображен на рис. 87, где изотермическое расширение и сжатие задано соответственно кривыми 1-2 и 3-4, а адиабатические расширение и сжатие — кривыми 2-3 и 4-1. При изотермическом процессе U = const, поэтому, согласно (54.4), количество теплоты Q₁, полученное газом от нагревателя, равно работе расширения А₁₂, совершаемой газом из состояния 1 в состояние 2:

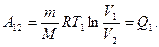(58.1)

В середине XIX в. возникла проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему и применяя к ней второе начало термодинамики, Клаузиус свел его содержание к утверждению, что энтропия Вселенной должна достигнуть своего максимума. Это означает, что со временем все формы движения должны перейти в тепловую. Переход же теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной сравняется, т. e. наступит полное тепловое равновесие и все процессы во Вселенной прекратятся — наступит тепловая смерть Вселенной. Ошибочность вывода о тепловой смерти заключается в том, что бессмысленно примерять второе начало термодинамики к незамкнутым системам, например к такой безграничной и бесконечно развивающейся системе, как Вселенная.

При адиабатическом расширении 2-3 теплообмен с .окружающей средой отсутствует и работа расширения А₂₃ совершается за счет изменения внутренней энергии (см. (55.1) и (55.8)):

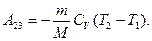
Теплота Q₂ отданная газом холодильнику при изотермическом сжатии, равна работе сжатия А₃₄:

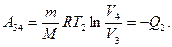(58.2)

Работа адиабатического сжатия

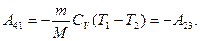
Работа, совершаемая в результате кругового процесса, и; как можно показать, определяется заштрихованной на рис. 87 площадью.

Термический к.п.д. цикла Карно, согласно (56.2),

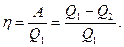
Применив уравнение (55.5) для адиабат 2-3 и 4-1, получим

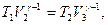
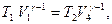
откуда

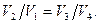(58.3)

Подставляя (58.1) и (58.2) в формулу (56.2) и учитывая (58.3), получим

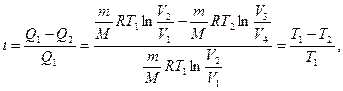(58.4)

т. е. для цикла Карно к.п.д. действительно определяется только температурой нагревателя и холодильника. Для его повышения необходимо увеличивать разность температур нагревателя и холодильника. Например, при T₁ = 400 К и T₂ = 300 К 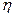= 0,25. Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то 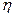= 0,5. К.п.д. всякого реального теплового двигателя ввиду трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.

Теорема Карно послужила основанием для установления термодинамической шкалы температур. Сравнив левую и правую части формулы (58.4), получим

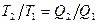, (58.5)

т. е. для сравнения температур T₁ и Т₂ двух тел необходимо осуществить обратимый цикл Карно, в котором одно тело используется в качестве нагревателя, и другое — холодильника. Из равенства (58.5) видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному количеству теплоты. Согласно теореме
Карно, химический состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шкала не связана со свойствами какого-то определенного термометрического вещества.

§ 59. Энтропия, ее статистическое толкование и связь с термодинамической вероятностью

Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом
участке процесса, равно 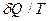. Строгий теоретический анализ показывает, что для любого обратимого кругового процесса сумма приведенных количеств теплоты равна нулю:

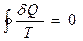. (59.1)

Из равенства нулю интеграла, взятого по замкнутому контуру (57.1), следует, что подынтегральное выражение dQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

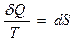. (59.2)

Функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается S.

Из формулы (59.1) следует, что для обратимых процессов изменение энтропии

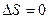. (59.3)

В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

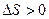. (59.4)

Отметим, что выражения (59.3) и (59.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (59.3) и (59.4) можно представить в виде неравенства Клаузиуса

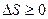, (59.5)

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (59.2) изменение энтропии

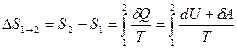, (59.6)

где подынтегральное выражение и пределы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (59.6) определяет энтропию лишь с точностью до аддитивной
постоянной, т. е. начало отсчета энтропии произвольно.

Исходя из выражения (59.6), найдем изменение энтропии в процессах идеального газа. Так как 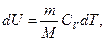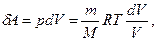то

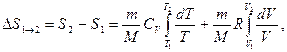
или

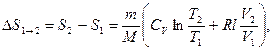
т.e. изменение энтропии 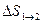идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1→2.

Так как для адиабатического процесса δQ = 0, то ∆S = 0 и, следовательно, S = const, т. e. адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы(59.7) следует, что при изотермическом процессе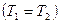

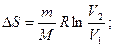
при изохорном процессе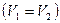

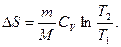
Так как реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. Этот принцип лежит в основе еще одной формулировки второго начала термодинамики: возможны лишь такие процессы, происходящие макроскопической системе, которые ведут к увеличению ее энтропии.

Физический смысл энтропии был выяснен Л. Больцманом, предположившим, что энтропия связана с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, 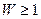, т.e. термодинамическая вероятность не есть вероятность в математическом смысле (последняя ≤ 1!)).

Формула Больцмана имеет следующий вид:

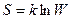, (59.8)

где k — постоянная Больцмана. Таким образом, энтропия, по Больцману, определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (59.8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих; данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.

Согласно представлениям термодинамики, процессы в замкнутой системе идут в сторону возрастания энтропии до максимума. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной.

Сопоставляя выражения (59.5) и (59.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).

Исходя из этого можно сформулировать второе начало термодинамики, отражая его статистический смысл: при необратимых процессах, происходящих в замкнутой системе, вероятность состояния системы возрастает, при обратимых же процессах — остается неизменной.