Адиабатический процесс

Адиабатическим называется процесс, при котором отсутствует теплообмен ( 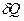= 0) между физической системой и окружающей средой. Близкими к адиабатическим являются все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.

Из первого начала термодинамики ( 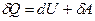) для адиабатического процесса следует, что

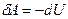, (55.1)

т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Таким образом, адиабатический процесс противоположен изотермическому, так как в последнем работой совершается за счет притока извне эквивалентного количества теплоты.

Используя выражения (52.1) и (53.4), для произвольной массы газа перепишем уравнение (55.1):

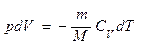. (55.2)

Продифференцировав уравнение состояния для идеального газа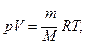

получим

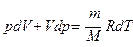. (55.3)

Исключим из (55.2) и (55.3) температуру Т:

.

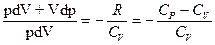Разделив переменные и учитывая, что 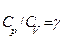(см. (53.8)), получим

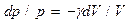
Интегрируя это уравнение в пределах от р₁ до р₂ и соответственно от V₁ до V₂ , а затем потенцируя, получим

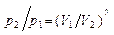, или .

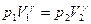Так как состояния 1 и 2 выбраны произвольно, то можно записать

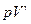= const. (55.4)

Полученное выражение есть уравнение газового состояния при адиабатическом процессе, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из (55.4) с помощью уравнения Клапейрона - Менделеева

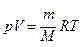
соответственно давление или объем:

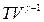= const, (55.5)

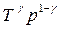= const. (55.6)

Выражения (55.4) — (55.6) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина (см. (53.8) и (53.2))

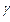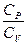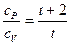= = . (55.7)

является коэффициентом Пуассона. Для одноатомных газов (Ne, Не и др.), достаточно хорошо удовлетворяющих условию идеальности, 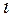= 3, 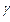= 1,67. Для двухатомных газов (Н₂, N₂, O₂ и др.) 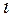= 5, 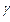= 1,4. Значения 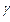, вычисленные по формуле (55.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис. 83). На рисунке видно, что адиабата ( 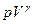= const) более крута, чем изотерма (pV= const). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Рис. 83

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение (55.2) в виде

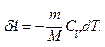
Если газ адиабатически расширяется от объема V₁ до V₂ , то его температура падает от T₁ до T₂ и работа расширения идеального газа

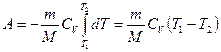. (55.8)

Применяя те же приемы, что и при выводе формулы (55.5), выражение (55.8) для работы при адиабатическом процессе можно преобразовать к виду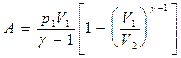

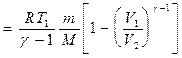
где .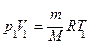

Работа, совершаемая газом при адиабатическом расширении 1-2 (определяется заштрихованной площадью на рис. 83), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность – они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны C_V и C_p в изотермическом процессе (dT=0) теплоемкость равна ±∞, в адиабатическом ( δQ=0 ) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const) можно вывести уравнение политропы:

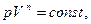(55.9)

где 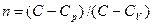- показатель политропы. Очевидно, что при С=0, n=γ, из (55.9) получается уравнение адиабаты; при С=∞, n=1 – уравнение изотермы; при С=С_р, n=0 – уравнение изобары, при С=С_V, n=±∞ - уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.