ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ НАГРУЗОК
1. Общие замечания
Важнейшим признаком динамического поведения деформируемой системы является появление сил инерции в ее элементах, резкое изменение скорости соприкасающихся с ними объектов. Наиболее эффектно это проявляется при ударе, который связан с возрастанием нагрузок до существенных величин за бесконечно малые отрезки времени.
Когда же силовые воздействия происходят в течение сравнительно длительного времени, изменяются по тем или иным четко детерминированным или статистическим законам , обычно говорят о процессах колебаний в конструкциях и системах. Это и затухающие колебания системы, «успокаивающейся» после удара, это и многочасовые колебания от действия работающих машин и механизмов и другие.
Общий подход к расчету элементов конструкций на динамическую нагрузку основан на использовании известного из теоретической механики принципа Даламбера, согласно которому движущееся тело можно рассматривать в состоянии динамического равновесия, если к действующим на него внешним силам добавить силы инерции. Силы инерции в ряде случаев могут быть определены непосредственно, например, при равноускоренном линейном перемещении, при вращении деталей машин, при колебаниях. В других случаях, в частности при ударе, для определения динамических напряжений и деформаций используется закон сохранения энергии.
При расчете влияние динамической нагрузки обычно учитывается с помощью так называемого коэффициента динамичности. Для получения максимального значения усилия, напряжения, деформации, перемещения и т.п. динамическая нагрузка заменяется статической, а найденные от нее напряжение, перемещение, деформация умножаются на коэффициент динамичности. КD.
2.Учет постоянных сил инерции.
При решении задач будем рассматривать движующуся систему в любой момент времени как находящуюся в равновесии под действием внешних сил, реакций связей и возникающих при ускоренном движении сил инерции.
Пример 1. Груз массой m = 3000 кг поднимается лебедкой, установленной на двух двутаврах №20 ( рис. 6.1) с постоянным ускорением а = 1 мс –2. Собственный все лебедки G = 5 кН. Проверить прочность балок при
l = 4 м; [s] = 160 мПа.

| |
При подъеме груза на балку действует усилие в тросе N и вес
лебедки G. Эпюра изгибающих моментов показана на рис. 6.1,б.
Усилие в тросе найдем из уравнения равновесия груза, записанного на основании принципа Даламбера (рис. 6.1,в)
N = G + J = mg + ma = mg (1+ 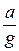 ) = N ст · КD,
) = N ст · КD,
где J – сила инерции,
Nст = m·g – усилие в тросе от веса груза,
КD = 1 + 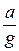 - коэффициент динамичности.
- коэффициент динамичности.
N = 3000 · 9, 8· ( 1 + 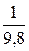 )· 10 -3 = 32,4 кН.
)· 10 -3 = 32,4 кН.
Максимальный момент в опасном сечении
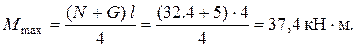
Геометрические характеристики двутавравра № 20 ( ГОСТ 8239 – 72)
Jx= 1840 см 4, Wx = 184 cм3.
Момент сопротивления составного сечения из двух двутавров
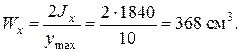
Максимальные напряжения
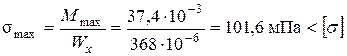 .
.
Дата добавления: 2021-07-22; просмотров: 491;











